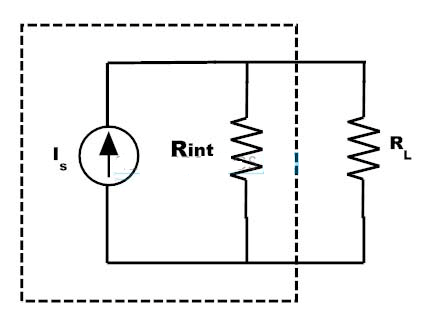
Practical Current Source

Similar to an ideal voltage source, an ideal current source also never exists as there is no device or source that delivers a constant current independent of connected load resistance or the voltage across the load terminals. However, if the load voltage is small, load current in practical current source and current from ideal current source are equal. Therefore, a real model or practical current source is obtained from an ideal current source in parallel with resistance (or internal resistance). This resembles , the current changes in a practical current source with change in voltage of the load (or change in resistance of the load).

Concept of Source Transformations

Consider both practical voltage and current sources with load resistance of RL. Let us see how the circuit behaves for resistance change at the load.

·         If the load resistance, RL = 0 in practical voltage source circuit, then the load acts as a short circuit and hence the short circuit current flows through the load. So the VL is zero (VL = IL * RL) and the IL would be

IL = Vs/Rs

·         Similarly for RL=0 in practical current source circuit, load also behaves as short circuit as it prefers the current flow through non-resistance path. This load current is equal to the source current Is which is equal to the value of Vs/Rs in practical voltage source circuit.

Therefore, Is = Vs/Rs when RL = 0…………(1)

 If the load resistance RL is infinity, both circuits behaves as an open circuit. Therefore load current is zero in both circuits. And the voltage drop across the resistance Rint in practical current source circuit is Is*Rint

Vint = Is * Rint

·         And the voltage across the Rs in a practical voltage source circuit is equal to the Vs which is equal to the Is* Rint of the practical current source circuit.

Vs = Is * Rint when RL is infinity ………………(2)

Hence from equations 1 and 2, we get

Vs = Rs * Is

Vs = Rint * Is

By observing above two equations, if the internal resistance of the two sources is same then the two sources are electrically equivalent. These two sources are equivalent , they can produce the same values of IL and VL when connected to same load resistance. Hence, these equivalent sources can produce identical values of short circuited current and open circuit voltage when zero load resistance and infinity resistances respectively. Therefore, by interchanging the internal resistors we can transform their properties from current source to a voltage source and vice-versa.