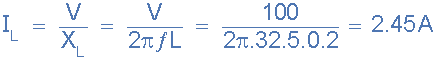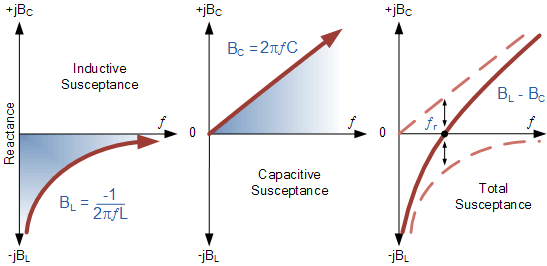
Susceptance at Resonance

From above, the inductive susceptance, B_L is inversely proportional to the frequency as represented by the hyperbolic curve. The capacitive susceptance, B_C is directly proportional to the frequency and is therefore represented by a straight line. The final curve shows the plot of total susceptance of the parallel resonance circuit versus the frequency and is the difference between the two susceptance’s.

Then we can see that at the resonant frequency point were it crosses the horizontal axis the total circuit susceptance is zero. Below the resonant frequency point, the inductive susceptance dominates the circuit producing a “lagging” power factor, whereas above the resonant frequency point the capacitive susceptance dominates producing a “leading” power factor.

So at the resonant frequency, ƒr the current drawn from the supply must be “in-phase” with the applied voltage as effectively there is only the resistance present in the parallel circuit, so the power factor becomes one or unity, ( θ = 0^o ).

Also as the impedance of a parallel circuit changes with frequency, this makes the circuit impedance “dynamic” with the current at resonance being in-phase with the voltage since the impedance of the circuit acts as a resistance. Then we have seen that the impedance of a parallel circuit at resonance is equivalent to the value of the resistance and this value must, therefore represent the maximum dynamic impedance (Z_d) of the circuit as shown.

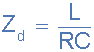
Current in a Parallel Resonance Circuit

As the total susceptance is zero at the resonant frequency, the admittance is at its minimum and is equal to the conductance, G. Therefore at resonance the current flowing through the circuit must also be at its minimum as the inductive and capacitive branch currents are equal ( I_L = I_C ) and are 180^o out of phase.

We remember that the total current flowing in a parallel RLC circuit is equal to the vector sum of the individual branch currents and for a given frequency is calculated as:

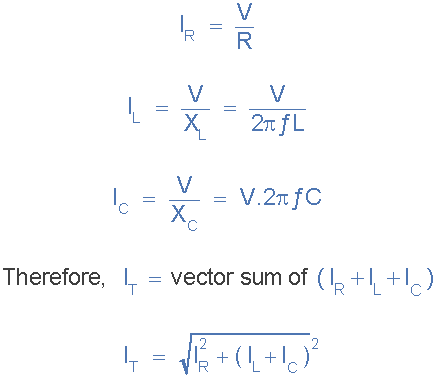
At resonance, currents I_L and I_C are equal and cancelling giving a net reactive current equal to zero. Then at resonance the above equation becomes.

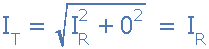
Since the current flowing through a parallel resonance circuit is the product of voltage divided by impedance, at resonance the impedance, Z is at its maximum value, ( =R ). Therefore, the circuit current at this frequency will be at its minimum value of V/R and the graph of current against frequency for a parallel resonance circuit is given as.

Parallel Circuit Current at Resonance

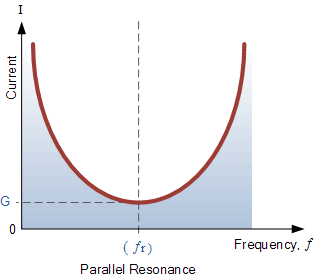
The frequency response curve of a parallel resonance circuit shows that the magnitude of the current is a function of frequency and plotting this onto a graph shows us that the response starts at its maximum value, reaches its minimum value at the resonance frequency when I_MIN = I_R and then increases again to maximum as ƒ becomes infinite.

The result of this is that the magnitude of the current flowing through the inductor, L and the capacitor, C tank circuit can become many times larger than the supply current, even at resonance but as they are equal and at opposition ( 180^o out-of-phase ) they effectively cancel each other out.

As a parallel resonance circuit only functions on resonant frequency, this type of circuit is also known as an Rejecter Circuit because at resonance, the impedance of the circuit is at its maximum thereby suppressing or rejecting the current whose frequency is equal to its resonant frequency. The effect of resonance in a parallel circuit is also called “current resonance”.

The calculations and graphs used above for defining a parallel resonance circuit are similar to those we used for a series circuit. However, the characteristics and graphs drawn for a parallel circuit are exactly opposite to that of series circuits with the parallel circuits maximum and minimum impedance, current and magnification being reversed. Which is why a parallel resonance circuit is also called an Anti-resonance circuit.

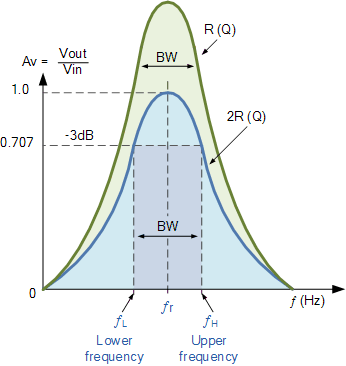
Bandwidth & Selectivity of a Parallel Resonance Circuit

The bandwidth of a parallel resonance circuit is defined in exactly the same way as for the series resonance circuit. The upper and lower cut-off frequencies given as: ƒ_upper and ƒ_lower respectively denote the half-power frequencies where the power dissipated in the circuit is half of the full power dissipated at the resonant frequency 0.5( I² R ) which gives us the same -3dB points at a current value that is equal to 70.7% of its maximum resonant value, ( 0.707 x I )² R

As with the series circuit, if the resonant frequency remains constant, an increase in the quality factor, Q will cause a decrease in the bandwidth and likewise, a decrease in the quality factor will cause an increase in the bandwidth as defined by:

  BW = ƒ_r /Q  or  BW = ƒ_upper - ƒ_lower

Also changing the ratio between the inductor, L and the capacitor, C, or the value of the resistance, R the bandwidth and therefore the frequency response of the circuit will be changed for a fixed resonant frequency. This technique is used extensively in tuning circuits for radio and television transmitters and receivers.

The selectivity or Q-factor for a parallel resonance circuit is generally defined as the ratio of the circulating branch currents to the supply current and is given as:

Note that the Q-factor of a parallel resonance circuit is the inverse of the expression for the Q-factor of the series circuit. Also in series resonance circuits the Q-factor gives the voltage magnification of the circuit, whereas in a parallel circuit it gives the current magnification.

Bandwidth of a Parallel Resonance Circuit

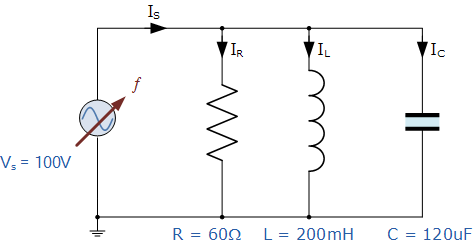
Parallel Resonance Example No1

A parallel resonance network consisting of a resistor of 60Ω, a capacitor of 120uF and an inductor of 200mH is connected across a sinusoidal supply voltage which has a constant output of 100 volts at all frequencies. Calculate, the resonant frequency, the quality factor and the bandwidth of the circuit, the circuit current at resonance and current magnification.

1. Resonant Frequency, ƒ_r

2. Inductive Reactance at Resonance, X_L

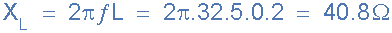
3. Quality factor, Q

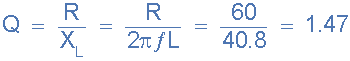
4. Bandwidth, BW

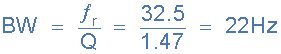
5. The upper and lower -3dB frequency points, ƒ_H and ƒ_L

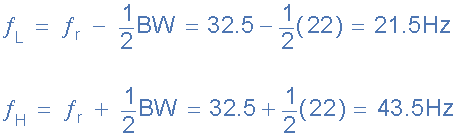
6. Circuit Current at Resonance, I_T

At resonance the dynamic impedance of the circuit is equal to R

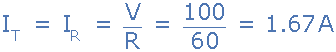
7. Current Magnification, I_mag

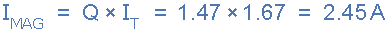
Note that the current drawn from the supply at resonance (the resistive current) is only 1.67 amps, while the current flowing around the LC tank circuit is larger at 2.45 amps. We can check this value by calculating the current flowing through the inductor (or capacitor) at resonance.