Radians

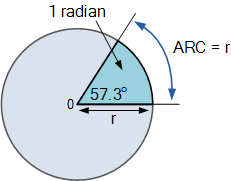
The Radian, (rad) is defined mathematically as a quadrant of a circle where the distance subtended on the circumference of the circle is equal to the length of the radius (r) of the same circle. Since the circumference of a circle is equal to 2π x radius, there must be 2π radians around the 360^o of a circle.

In other words, the radian is a unit of angular measurement and the length of one radian (r) will fit 6.284 (2*π) times around the whole circumference of a circle. Thus one radian equals 360^o/2π = 57.3^o. In electrical engineering the use of radians is very common so it is important to remember the following formula.

Definition of a Radian

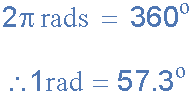
Using radians as the unit of measurement for a sinusoidal waveform would give 2π radians for one full cycle of 360^o. Then half a sinusoidal waveform must be equal to 1π radians or just π (pi). Then knowing that pi, (π) is equal to 3.142, the relationship between degrees and radians for a sinusoidal waveform is therefore given as:

Relationship between Degrees and Radians

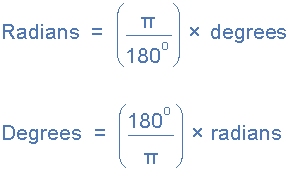
Applying these two equations to various points along the waveform gives us.

The conversion between degrees and radians for the more common equivalents used in sinusoidal analysis are given in the following table.

Relationship between Degrees and Radians

The velocity at which the generator rotates around its central axis determines the frequency of the sinusoidal waveform. As the frequency of the waveform is given as ƒ Hz or cycles per second, the waveform also has angular frequency, ω, (Greek letter omega), in radians per second. Then the angular velocity of a sinusoidal waveform is given as.

Angular Velocity of a Sinusoidal Waveform

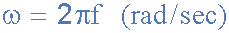
and in the United Kingdom, the angular velocity or frequency of the mains supply is given as:

in the USA as their mains supply frequency is 60Hz it can be given as: 377 rad/s

So we now know that the velocity at which the generator rotates around its central axis determines the frequency of the sinusoidal waveform and which can also be called its angular velocity, ω. But we should by now also know that the time required to complete one full revolution is equal to the periodic time, (T) of the sinusoidal waveform.

As frequency is inversely proportional to its time period, ƒ = 1/T we can therefore substitute the frequency quantity in the above equation for the equivalent periodic time quantity and substituting gives us.

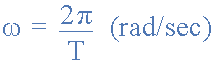
The above equation states that for a smaller periodic time of the sinusoidal waveform, the greater must be the angular velocity of the waveform. Likewise in the equation above for the frequency quantity, the higher the frequency the higher the angular velocity.

Sinusoidal Waveform Example No1

A sinusoidal waveform is defined as: V_m = 169.8 sin(377t) volts. Calculate the RMS voltage of the waveform, its frequency and the instantaneous value of the voltage, (V_i) after a time of six milliseconds (6ms).

We know from above that the general expression given for a sinusoidal waveform is:

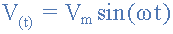
Then comparing this to our given expression for a sinusoidal waveform above of V_m = 169.8 sin(377t) will give us the peak voltage value of 169.8 volts for the waveform.

The waveforms RMS voltage is calculated as:

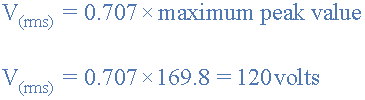
The angular velocity (ω) is given as 377 rad/s. Then 2πƒ = 377. So the frequency of the waveform is calculated as:

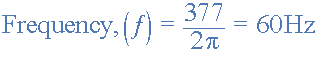
The instantaneous voltage V_i value after a time of 6mS is given as:

Note that the angular velocity at time t = 6mS is given in radians (rads). We could, if so wished, convert this into an equivalent angle in degrees and use this value instead to calculate the instantaneous voltage value. The angle in degrees of the instantaneous voltage value is therefore given as:

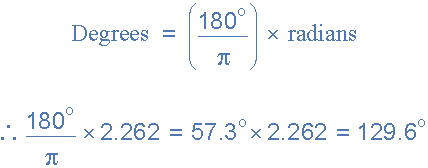
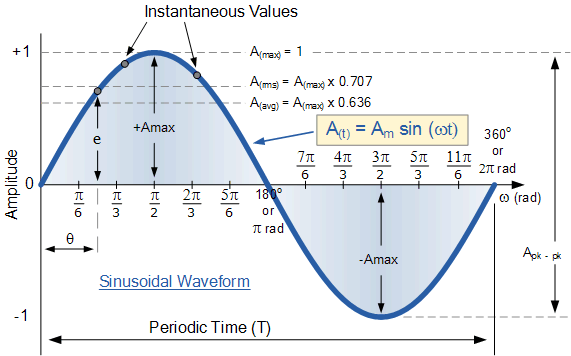
Sinusoidal Waveform

Then the generalised format used for analysing and calculating the various values of a Sinusoidal Waveform is as follows:

A Sinusoidal Waveform

In the next tutorial about Phase Difference we will look at the relationship between two sinusoidal waveforms that are of the same frequency but pass through the horizontal zero axis at different time intervals.