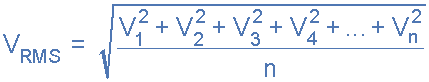
The RMS Value of an AC Waveform

The average value of an AC waveform that we calculated above as being: 0.637*V_max is NOT the same value we would use for a DC supply. This is because unlike a DC supply which is constant and and of a fixed value, an AC waveform is constantly changing over time and has no fixed value. Thus the equivalent value for an alternating current system that provides the same amount of electrical power to a load as a DC equivalent circuit is called the “effective value”.

The effective value of a sine wave produces the same I²*R heating effect in a load as we would expect to see if the same load was fed by a constant DC supply. The effective value of a sine wave is more commonly known as the Root Mean Squared or simply RMS value as it is calculated as the square root of the mean (average) of the square of the voltage or current.

That is V_rms or I_rms is given as the square root of the average of the sum of all the squared mid-ordinate values of the sine wave. The RMS value for any AC waveform can be found from the following modified average value formula as shown.

RMS Value of an AC Waveform

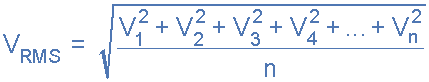
Where: n equals the number of mid-ordinates.

For a pure sinusoidal waveform this effective or R.M.S. value will always be equal too: 1/√2*V_max which is equal to 0.707*V_max and this relationship holds true for RMS values of current. The RMS value for a sinusoidal waveform is always greater than the average value except for a rectangular waveform. In this case the heating effect remains constant so the average and the RMS values will be the same.

One final comment about R.M.S. values. Most multimeters, either digital or analogue unless otherwise stated only measure the R.M.S. values of voltage and current and not the average. Therefore when using a multimeter on a direct current system the reading will be equal to I = V/R and for an alternating current system the reading will be equal to Irms = Vrms/R.

Also, except for average power calculations, when calculating RMS or peak voltages, only use V_RMS to find I_RMS values, or peak voltage, Vp to find peak current, Ip values. Do not mix them together as Average, RMS or Peak values of a sine wave are completely different and your results will definitely be incorrect.

Form Factor and Crest Factor

Although little used these days, both Form Factor and Crest Factor can be used to give information about the actual shape of the AC waveform. Form Factor is the ratio between the average value and the RMS value and is given as.

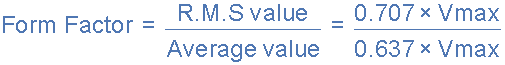
For a pure sinusoidal waveform the Form Factor will always be equal to 1.11. Crest Factor is the ratio between the R.M.S. value and the Peak value of the waveform and is given as.

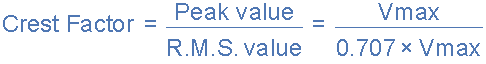
For a pure sinusoidal waveform the Crest Factor will always be equal to 1.414.

AC Waveform Example No2

A sinusoidal alternating current of 6 amps is flowing through a resistance of 40Ω. Calculate the average voltage and the peak voltage of the supply.

The R.M.S. Voltage value is calculated as:

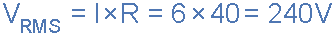
The Average Voltage value is calculated as:

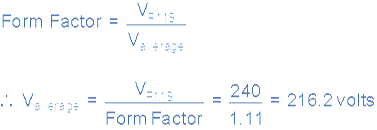
The Peak Voltage value is calculated as:

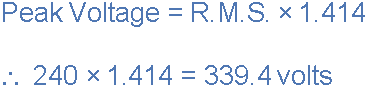
The use and calculation of Average, R.M.S, Form factor and Crest Factor can also be use with any type of periodic waveform including Triangular, Square, Sawtoothed or any other irregular or complex voltage/current waveform shape. Conversion between the various sinusoidal values can sometimes be confusing so the following table gives a convenient way of converting one sine wave value to another.

Sinusoidal Waveform Conversion Table

In the next tutorial about Sinusoidal Waveforms we will look at the principal of generating a sinusoidal AC waveform (a sinusoid) along with its angular velocity representation.