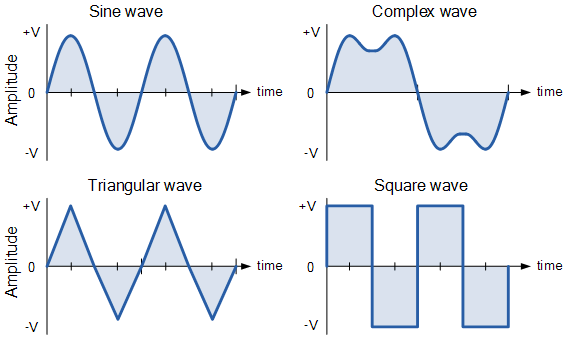
Types of Periodic Waveform

The time taken for an AC Waveform to complete one full pattern from its positive half to its negative half and back to its zero baseline again is called a Cycle and one complete cycle contains both a positive half-cycle and a negative half-cycle. The time taken by the waveform to complete one full cycle is called the Periodic Time of the waveform, and is given the symbol “T”.

The number of complete cycles that are produced within one second (cycles/second) is called the Frequency, symbol ƒ of the alternating waveform. Frequency is measured in Hertz, ( Hz ) named after the German physicist Heinrich Hertz.

Then we can see that a relationship exists between cycles (oscillations), periodic time and frequency (cycles per second), so if there are ƒ number of cycles in one second, each individual cycle must take 1/ƒ seconds to complete.

Relationship Between Frequency and Periodic Time

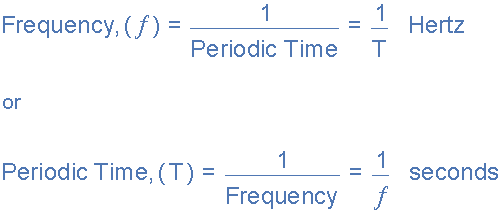
AC Waveform Example No1

1. What will be the periodic time of a 50Hz waveform and 2. what is the frequency of an AC waveform that has a periodic time of 10mS.

1).

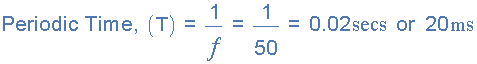
2).

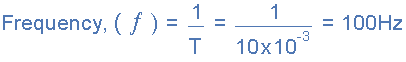
Frequency used to be expressed in “cycles per second” abbreviated to “cps”, but today it is more commonly specified in units called “Hertz”. For a domestic mains supply the frequency will be either 50Hz or 60Hz depending upon the country and is fixed by the speed of rotation of the generator. But one hertz is a very small unit so prefixes are used that denote the order of magnitude of the waveform at higher frequencies such as kHz, MHz and even GHz.

Definition of Frequency Prefixes

Amplitude of an AC Waveform

As well as knowing either the periodic time or the frequency of the alternating quantity, another important parameter of the AC waveform is Amplitude, better known as its Maximum or Peak value represented by the terms, Vmax for voltage or Imax for current.

The peak value is the greatest value of either voltage or current that the waveform reaches during each half cycle measured from the zero baseline. Unlike a DC voltage or current which has a steady state that can be measured or calculated using Ohm’s Law, an alternating quantity is constantly changing its value over time.

For pure sinusoidal waveforms this peak value will always be the same for both half cycles ( +Vm = -Vm ) but for non-sinusoidal or complex waveforms the maximum peak value can be very different for each half cycle. Sometimes, alternating waveforms are given a peak-to-peak, Vp-p value and this is simply the distance or the sum in voltage between the maximum peak value, +Vmax and the minimum peak value, -Vmax during one complete cycle.

The Average Value of an AC Waveform

The average or mean value of a continuous DC voltage will always be equal to its maximum peak value as a DC voltage is constant. This average value will only change if the duty cycle of the DC voltage changes. In a pure sine wave if the average value is calculated over the full cycle, the average value would be equal to zero as the positive and negative halves will cancel each other out. So the average or mean value of an AC waveform is calculated or measured over a half cycle only and this is shown below.

Average Value of a Non-sinusoidal Waveform

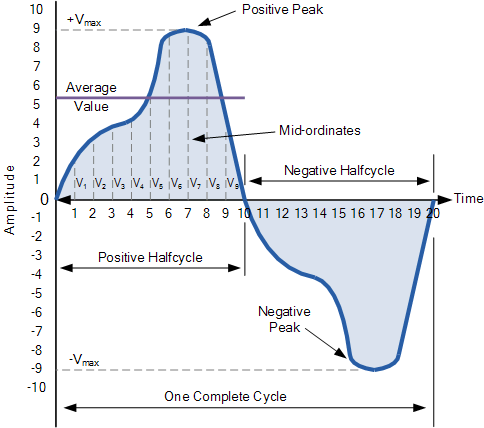
To find the average value of the waveform we need to calculate the area underneath the waveform using the mid-ordinate rule, trapezoidal rule or the Simpson’s rule found commonly in mathematics. The approximate area under any irregular waveform can easily be found by simply using the mid-ordinate rule.

The zero axis base line is divided up into any number of equal parts and in our simple example above this value was nine, ( V₁ to V₉ ). The more ordinate lines that are drawn the more accurate will be the final average or mean value. The average value will be the addition of all the instantaneous values added together and then divided by the total number. This is given as.

Average Value of an AC Waveform

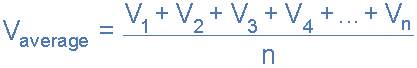
Where: n equals the actual number of mid-ordinates used.

For a pure sinusoidal waveform this average or mean value will always be equal to 0.637*V_max and this relationship also holds true for average values of current.