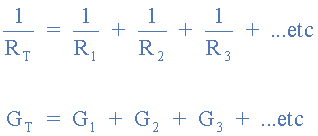
Current Division using Conductances

Another simple method of finding the branch currents in a parallel circuit is to use the conductance method. In DC circuits, Conductance is the reciprocal of resistance, and is denoted by the letter “G“. As conductance (G) is the reciprocal of resistance (R) which is measured in Ohm’s (Ω), the reciprocal of Ohm’s is called “mho” (℧), (an inverted ohm sign). Thus G = 1/R. The electrical units given to conductance is the Siemen (symbol S).

So for parallel connected resistors, the equavalent or total conductance, C_T will be equal to the sum of the individual conductances as shown.

Parallel Conductance

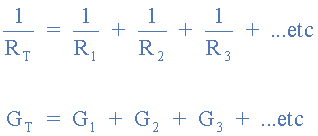
Therefore, if a resistance has a fixed value of 10Ω, it will have an equivalent conductance of 0.1S and so on. Because of the reciprocal, a high value of conductance represents a low value of resistance, and vice versa. We can also use prefixes in the form of milli-Siemens, mS, micro-Siemens, uS and even nano-Siemens, nS for very small conductances. So a resistor of 10kΩ will have a conductance of 100uS.

Using the Ohm’s Law equation for current in which I = V/R, we can define the branch currents using conductance as being: I = V*G

In fact we can take this one step further by saying that the supply current to a our parallel resisive network above is:

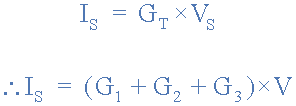
But we know from above that for a parallel connected circuit, voltage is common to all components and as voltage equals current times resistance, V = I*R, we can therefore conclude that when using conductance, the voltage is equal to current divided by conductance. That is V = I/G.

Then we can express the above equations for the current divider rule in relationship to conductance (G), instead of the resistance (R) as being:

Current Divider Rule using Conductance

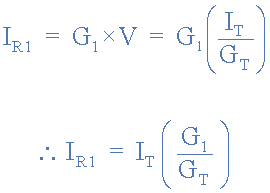
Likewise for the currents in parallel resistors R₂ and R₃ are given as:

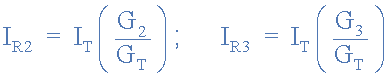
You may have noticed that unlike the equations above for resistance, each branch current has the same conductance in its numerator. That is to solve for I₁ we use G₁, and to solve for I₂ we use G₂. This is because the conductances are the reciprocals of the resistances.

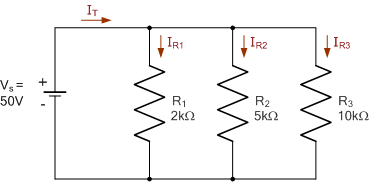
Current Divider Example No3

Using the conductance method, find the individual branch currents, I₁, I₂ and I₃ of the following parallel resistive circuit.

Total conductance G_T

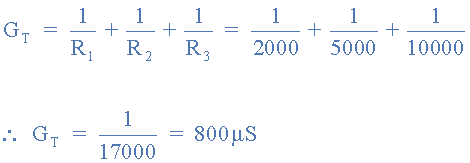
Total supply current I_S

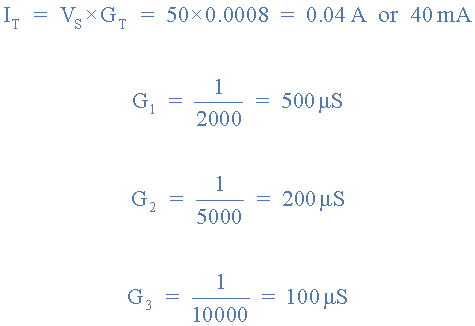
Individual branch currents I₁, I₂ and I₃

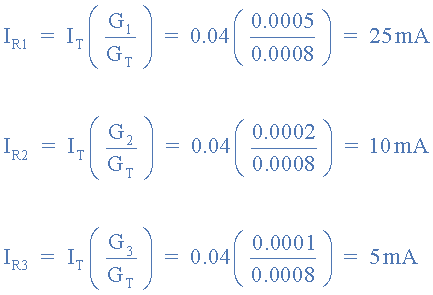
As conductance is the reciprocal or inverse of resistance, the equivalent resistance value of the example circuit is simply 1/800uS which equals 1250Ω or 1.25kΩ, which is clearly less than the smallest resistor value of R₁ at 2kΩ.

Current Divider Summary

Current dividers or current division is the process of finding the individual branch currents in a parallel circuit were each parallel element has the same voltage. Kirchhoff’s current law, (KCL) states that the algebraic sum of the individual currents entering a junction or node will equal the currents leaving it. That is the net result is zero.

Kirchhoff’s current divider rule can also be used to find individual branch currents when the equivalent resistance and the total circuit current are known. When only two resistive branches are involved, the current in one branch will be some fraction of the total current I_T. If the two parallel resistive branches are of equal value, the current will divide equally.

In the case of three or more parallel branches, the equivalent resistance R_EQ is used to divide the total current into the fractional currents for each branch producing a current ratio which is equal to the inverse of their resistive values resulting in the smaller value resistance having the greatest share of the current. The supply or total current, I_T being the sum of all the individual branch currents. This then makes current dividers useful for use with current sources.

It is sometimes convenient to use conductance with parallel circuits as it can help reduce the maths required for determining the branch currents through individual circuit elements that are connected together in parallel. This is because for parallel circuits the total conductance is the sum of the individual conductance values. Conductance is the reciprocal or inverse of resistance as G = 1/R. The units for conductance are Siemens, S. The conductance of an element can also be used even if the supply voltage is DC or AC for current dividers.