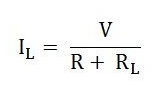
Millman’s Theorem

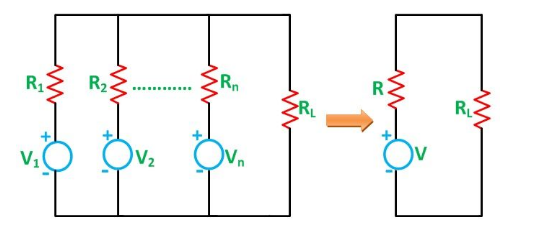
The Millman’s Theorem states that – when a number of voltage sources (V1, V2, V3……… Vn) are in parallel having internal resistance (R1, R2, R3………….Rn) respectively, the arrangement can replace by a single equivalent voltage source V in series with an equivalent series resistance R.  In other words; it determines the voltage across the parallel branches of the circuit, which have more than one voltage sources, i.e.,  reduces the complexity of the electrical circuit.

This Theorem is given by Jacob Millman. The utility of Millman’s Theorem is that the number of parallel voltage sources can be reduced to one equivalent source. It is applicable only to solve the parallel branch with one resistance connected to one voltage source or current source. It is also used in solving network having an unbalanced bridge circuit.

As per Millman’s Theorem

Explanation of Millman’s Theorem

Assuming a DC network of numerous parallel voltage sources with internal resistances supplying power to a load resistance RL as shown in the figure below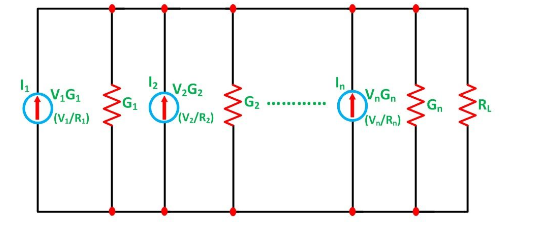

Let I represent the resultant current of the parallel current sources while G the equivalent conductance as shown in the figure below

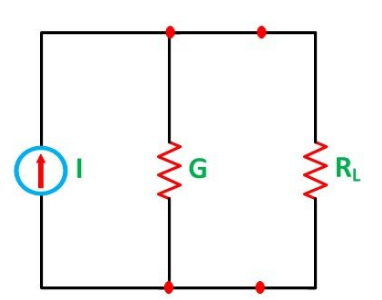
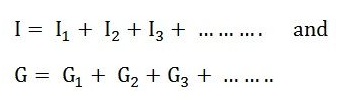
Next, the resulting current source is converted to an equivalent voltage source as shown in the figure below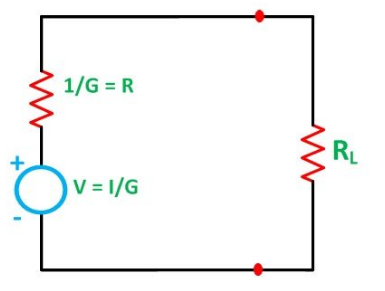

Thus,

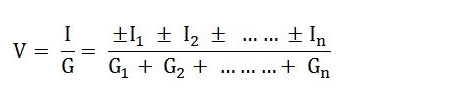
Positive (+) and negative (-) sign appeared to include the cases where the sources may not be supplying current in the same direction.

Also,

Where R is the equivalent resistance connected to the equivalent voltage source in series.

Thus, the final equation becomes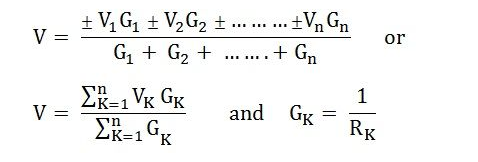

Steps for Solving Millman’s Theorem

Following steps are used to solve the network by Millman’s Theorem

Step 1 – Obtain the conductance (G1, G2,….) of each voltage source (V1, V2,….).

Step 2 – Find the value of equivalent conductance G by removing the load from the network.

Step 3 – Now, apply Millman’s Theorem to find the equivalent voltage source V by the equation shown below

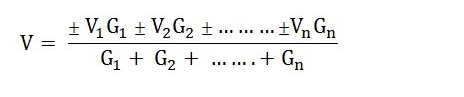
Step 4 – Determine the equivalent series resistance (R) with the equivalent voltage sources (V) by the equation

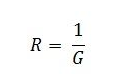
Step 5 – Find the current IL flowing in the circuit across the load resistance RL by the equation