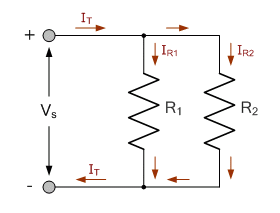
Current Dividers
Current Divider circuits have two or more parallel branches for currents to flow through but the voltage is the same for all components in the parallel cicruit

Current Divider Circuits are parallel circuits in which the source or supply current divides into a number of parallel paths. In a parallel connected circuit, all the components have their terminals connected together sharing the same two end nodes. This results in different paths and branches for the current to flow or pass along. However, the currents can have different values through each component.
The main characteristic of parallel circuits is that while they may produce different currents flowing through different branches, the voltage is common to all the connected paths. That is VR1 = VR2 = VR3 … etc. Therefore the need to find the individual resistor voltages is eliminated allowing branch currents to be easily found with Kirchhoff’s Current Law, (KCL) and of course Ohm’s Law.
The easiest to understand, and most basic form of a passive current divider network is that of two resistors connected together in parallel. The Current Divider Rule allows us to calculate the current flowing through each parallel resistive branch as a percentage of the total current. Consider the circuit below.
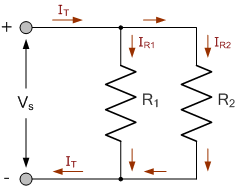
Here this basic current divider circuit consists of two resistors: R1, and R2 in parallel which splits the supply or source current IS between them into two separate currents IR1 and IR2 before joining together again and returning back to the source.
As the source or total current equals the sum of the individual branch currents, then the total current, IT flowing in the circuit is given by Kirchoffs current law KCL as being:
IT = IR1 + IR2
As the two resistors are connected in parallel, for Kirchhoff’s Current Law, (KCL) to hold true it must therefore follow that the current flowing through resistor R1 will be equal to:
IR1 = IT – IR2
and the current flowing through resistor R2 will be equal to:
IR2 = IT – IR1
As the same voltage, (V) is present across each resistive element, we can find the current flowing through each resistor in terms of this common voltage as it is simply V = I*R following Ohm’s Law. So solving for the voltage (V) across the parallel combination gives us:
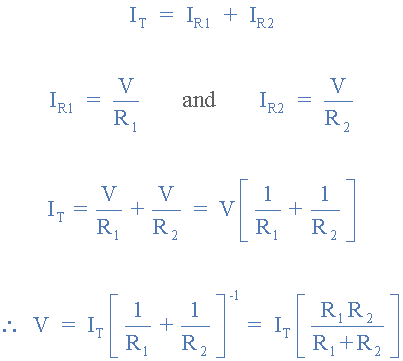
Solving for IR1 gives:
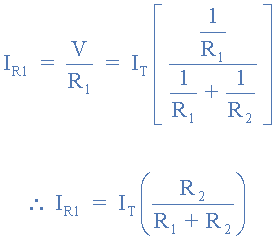
Likewise, solving for IR2 gives:
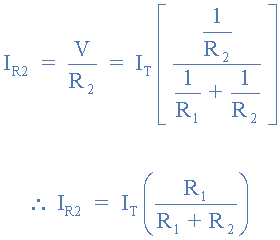
Notice that the above equations for each branch current has the opposite resistor in its numerator. That is to solve for I1 we use R2, and to solve for I2 we use R1. This is because each branch current is inversely proportional to its resistance resulting in the smaller resistance having the larger current.
A 20Ω resistor is connected in parallel with a 60Ω resistor. If the combination is connected across a 30 volts battery supply, find the current flowing through each resistor and the total current supplied by the source.
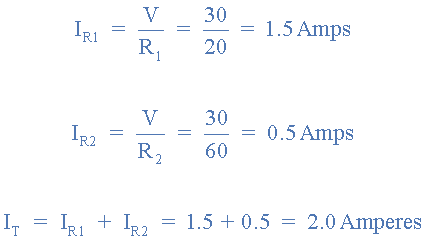
Note that the smaller 20Ω resistor has the larger current because by its very nature, a greater current will always flow through the path or branch of least resistance. This implies then that a short-circuit will produce maximum current flow, while an open-circuit will result in zero current flow. Remember also that the equivalent resistance, REQ of parallel connected resistors will always be less than the ohmic value of the smallest resistor with the equivalent resistance decreasing as more parallel resistances are added.
Sometimes it is not necessary to calculate all the branch currents, if the supply or total current, IT is already known, then the final branch current can be found by simply subtracting the calculated currents from the total current as defined by Kirchhoffs current law.
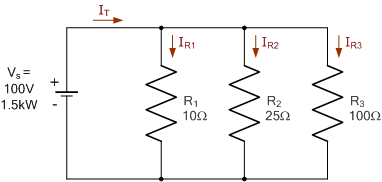
Three resistors are connected together to form a current divider circuit as shown below. If the circuit is fed from a 100 volts 1.5kW power supply, calculate the individual branch currents using the current division rule and the equivalent circuit resistance.
1) Total circuit current IT
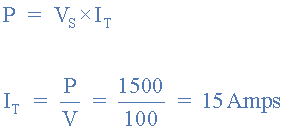
2) Equivalent resistance REQ
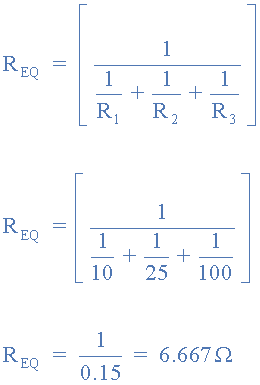
3) Branch currents IR1, IR2, IR3
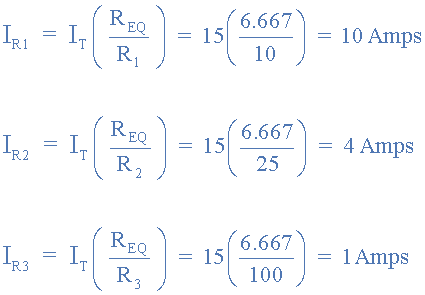
We can check our calculations as according to Kirchhoff’s Current Rule, all the branch currents will be equal to the total current, so: IT = IR1 + IR2 + IR3 = 10 + 4 + 1 = 15 amperes, as expected. Thus we can see that the total current, IT is divided according to a simple ratio determined by the branch resistances. Also, as the number of resistors connected in parallel increases, the supply ot total current, IT will also increase for a given supply voltage, VS as there are more parallel branches taking current.