Phasors

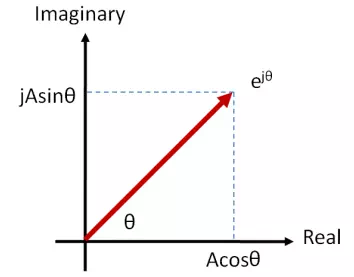
Figure One: Rectangular Notation

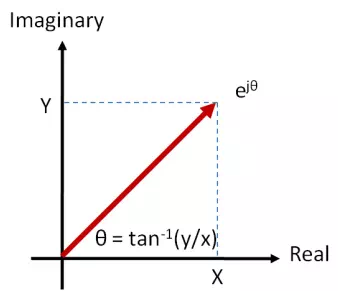
Figure Two: Polar Notation

Phasors provide a simple means of analysing linear circuits. At the heart of phasor analysis lies Euler’s formula1 :

A complex exponential can also be expressed as

It contains information about the magnitude and phase of a sinusoidal signal, but not the frequency or time. This simplifies use in circuit analysis, since most of the time, all quantities in the circuit will have the same frequency. (For circuits with sources at different frequencies, the principle of superposition must be used.)

A shorthand phasor notation is:

Note that this is simply a polar form, and can be converted to rectangular notation by (see figure one):

and back again by (see figure two):

Let us understand how this process works, even though a phasor causes circuits to heat up steady flow in current will explain on a basis that disallows overheating. Since according to the formula the outcome will be there is a time in duration which the current usage stays the same.