Capacitors in Parallel

Let us observe what happens, when few capacitors are connected in Parallel. Let us consider three capacitors with different values, as shown in the figure below.

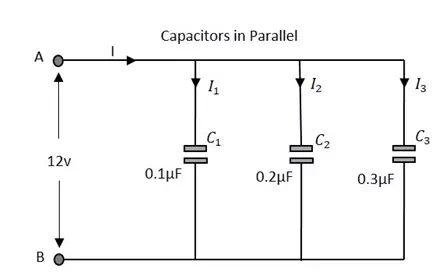
Capacitance

The total Capacitance of the circuit is the equivalent to the sum of the individual capacitances of the capacitors in the network.

CT=C1+C2+C3CT=C1+C2+C3

Where C₁ is the capacitance across the 1^st capacitor, C₂ is the capacitance across the 2^nd capacitor and C₃ is the capacitance across the 3^rd capacitor in the above network.

Voltage

The voltage measured at the end of the circuit is same as the voltage across all the capacitors that are connected in a parallel circuit.

VT=V1=V2=V3VT=V1=V2=V3

Where V_c1 is the voltage across the 1^st capacitor, V_c2 is the voltage across the 2^nd capacitor and V_c3 is the voltage across the 3^rd capacitor in the above network.

Current

The total current flowing is equal to the sum of the currents flowing through each capacitor connected in the parallel network.

IT=I1+I2+I3IT=I1+I2+I3

Where I₁ is the current through the 1^st capacitor, I₂ is the current through the 2^nd capacitor and I₃ is the current through the 3^rd capacitor in the above network.