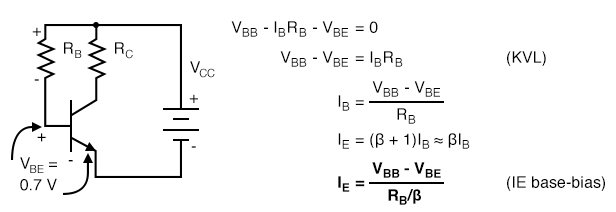
Transistor Biasing Calculations

Base Bias Resistor

The simplest biasing applies a base-bias resistor between the base and a base battery VBB. It is convenient to use the existing VCC supply instead of a new bias supply. An example of an audio amplifier stage using base-biasing is “Crystal radio with one transistor . . . ” crystal radio, Ch 9. Note the resistor from the base to the battery terminal. A similar circuit is shown in the figure below. Write a KVL (Kirchhoff’s voltage law) equation about the loop containing the battery, RB, and the VBE diode drop on the transistor in Figure below. Note that we use VBB for the base supply, even though it is actually VCC. If β is large we can make the approximation that IC =IE. For silicon transistors VBE≅0.7V.

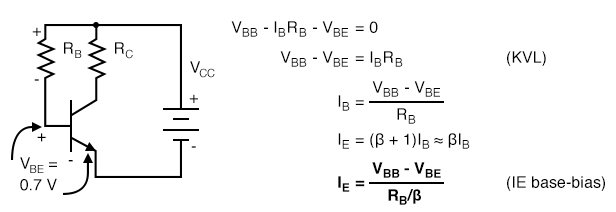
Base-bias

Silicon small signal transistors typically have a β in the range of 100-300.

Example Calculations:

Assuming that we have a β=100 transistor, what value of the base-bias resistor is required to yield an emitter current of 1mA? Solving the IE base-bias equation for RB and substituting β, VBB, VBE, and IE yield 930kΩ. The closest standard value is 910kΩ.

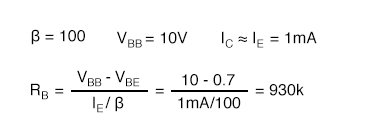
What is the emitter current with a 910kΩ resistor? What is the emitter current if we randomly get a β=300 transistor?

The emitter current is little changed in using the standard value 910kΩ resistor. However, with a change in β from 100 to 300, the emitter current has tripled. This is not acceptable in a power amplifier if we expect the collector voltage to swing from near VCC to near ground. However, for low level signals from micro-volts to about a volt, the bias point can be centered for a β of the square root of (100·300)=173. The bias point will still drift by a considerable amount. However, low-level signals will not be clipped.

Base-bias is not suitable for high emitter currents, as used in power amplifiers. The base-biased emitter current is not temperature stable.

Thermal runaway is the result of high emitter current causing a temperature increase which causes an increase in emitter current, which further increases temperature.

Collector-Feedback Bias

Variations in bias due to temperature and beta may be reduced by moving the VBB end of the base-bias resistor to the collector as in the figure below. If the emitter current were to increase, the voltage drop across RC increases, decreasing VC, decreasing IB fed back to the base. This, in turn, decreases the emitter current, correcting the original increase.

Write a KVL equation about the loop containing the battery, RC, RB, and the VBE drop. Substitute IC≅IE and IB≅IE/β. Solving for IE yields the IE CFB-bias equation. Solving for IB yields the IB CFB-bias equation.

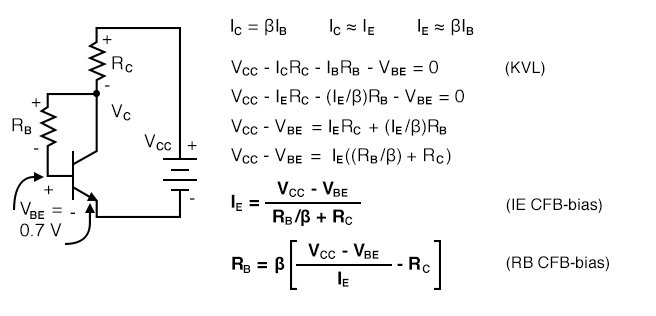
Collector-feedback bias.

Example Calculations:

Find the required collector feedback bias resistor for an emitter current of 1 mA, a 4.7K collector load resistor, and a transistor with β=100. Find the collector voltage VC. It should be approximately midway between VCC and ground.

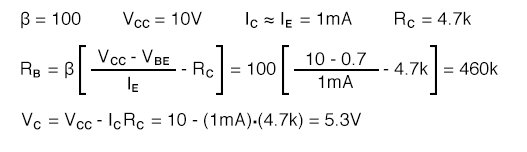
The closest standard value to the 460kΩ collector feedback bias resistor is 470kΩ. Find the emitter current IE with the 470KΩ resistor. Recalculate the emitter current for a transistor with β=100 and β=300.

We see that as beta changes from 100 to 300, the emitter current increases from 0.989mA to 1.48mA. This is an improvement over the previous base-bias circuit which had an increase from 1.02mA to 3.07mA. Collector feedback bias is twice as stable as base-bias with respect to beta variation.

Emitter-Bias

Inserting a resistor RE in the emitter circuit as in figure below causes degeneration, also known as negative feedback. This opposes a change in emitter current IE due to temperature changes, resistor tolerances, beta variation, or power supply tolerance. Typical tolerances are as follows: resistor— 5%, beta— 100-300, power supply— 5%. Why might the emitter resistor stabilize a change in current? The polarity of the voltage drop across RE is due to the collector battery VCC. The end of the resistor closest to the (-) battery terminal is (-), the end closest to the (+) terminal it (+). Note that the (-) end of RE is connected via VBB battery and RB to the base. Any increase in current flow through RE will increase the magnitude of negative voltage applied to the base circuit, decreasing the base current, decreasing the emitter current. This decreasing emitter current partially compensates the original increase.

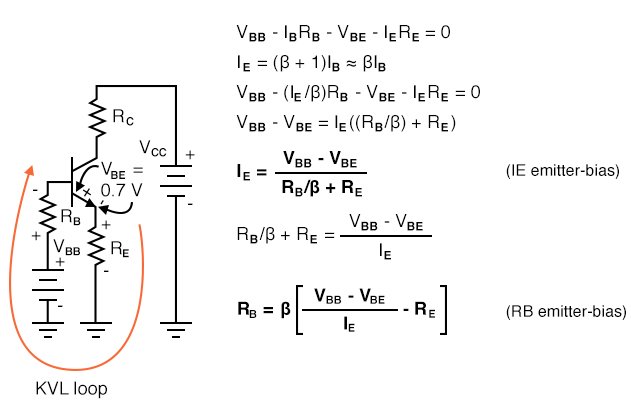
Emitter-bias

Note that base-bias battery VBB is used instead of VCC to bias the base in the figure above. Later we will show that the emitter-bias is more effective with a lower base bias battery. Meanwhile, we write a KVL equation for the loop through the base-emitter circuit, paying attention to the polarity on the components. We substitute IB≅IE/β and solve for emitter current IE. This equation can be solved for RB, equation: RB emitter-bias, Figure above.

Before applying the equations: RB emitter-bias and IE emitter-bias, the figure above, we need to choose values for RC and RE. RC is related to the collector supply VCC and the desired collector current IC which we assume is approximately the emitter current IE.

Normally the bias point for VC is set to half of VCC. Though, it could be set higher to compensate for the voltage drop across the emitter resistor RE. The collector current is whatever we require or choose. It could range from micro-Amps to Amps depending on the application and transistor rating. We choose IC = 1mA, typical of a small-signal transistor circuit.

Example Calculations:

We calculate a value for RC and choose a close standard value. An emitter resistor which is 10-50% of the collector load resistor usually works well.

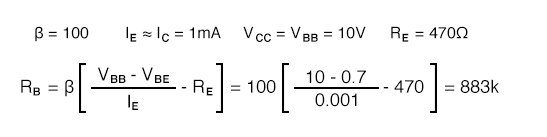
An 883k resistor was calculated for RB, an 870k chosen. At β=100, IE is 1.01mA.

For β=300 the emitter currents are shown in Table below.

Emitter current comparison for β=100, β=300.

The table above shows that for VBB = 10V, emitter-bias does not do a very good job of stabilizing the emitter current. The emitter-bias example is better than the previous base-bias example, but not by much. The key to effective emitter bias is lowering the base supply VBB nearer to the amount of emitter bias.

Rounding that is emitter current times emitter resistor: IERE = (1mA)(470) = 0.47V. In addition, we need to overcome the VBE = 0.7V. Thus, we need a VBB >(0.47 + 0.7)V or >1.17V. If emitter current deviates, this number will change compared with the fixed base supply VBB,causing a correction to base current IB and emitter current IE. A good value for VB >1.17V is 2V.

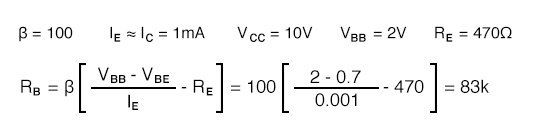
The calculated base resistor of 83k is much lower than the previous 883k. We choose 82k from the list of standard values. The emitter currents with the 82k RB for β=100 and β=300 are:

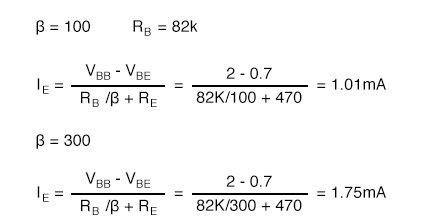
Comparing the emitter currents for emitter-bias with VBB = 2V at β=100 and β=300 to the previous bias circuit examples in the table below, we see considerable improvement at 1.75mA, though, not as good as the 1.48mA of collector feedback.

Emitter current comparison for β=100, β=300.

To improve performance of emitter-bias, either increase the emitter resistor RE or decrease the base-bias supply VBB or both.

As an example, we double the emitter resistor to the nearest standard value of 910Ω.

The calculated RB = 39k is a standard value resistor. No need to recalculate IE for β = 100. For β = 300, it is:

The performance of the emitter-bias circuit with a 910 emitter resistor is much improved. See Table below.

Emitter current comparison for β=100, β=300.

As an exercise, rework the emitter-bias example with the emitter resistor reverted back to 470Ω, and the base-bias supply reduced to 1.5V.

The 33k base resistor is a standard value, emitter current at β = 100 is OK. The emitter current at β = 300 is:

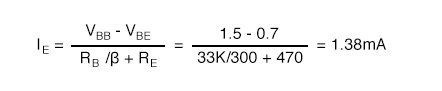
The table below compares the exercise results 1mA and 1.38mA to the previous examples.

Emitter current comparison for β=100, β=300.

The emitter-bias equations have been repeated in the figure below with the internal emitter resistance included for better accuracy. The internal emitter resistance is the resistance in the emitter circuit contained within the transistor package. This internal resistance rEE is significant when the (external) emitter resistor RE is small, or even zero. The value of internal resistance REE is a function of emitter current IE, Table below.

Derivation of rEE

rEE = KT/IEm where: K=1.38×10-23 watt-sec/oC, Boltzman's constant T= temperature in Kelvins ≅300. IE = emitter current m = varies from 1 to 2 for Silicon rEE ≅ 0.026V/IE = 26mV/IE

For reference the 26mV approximation is listed as equation rEE in Figure below.

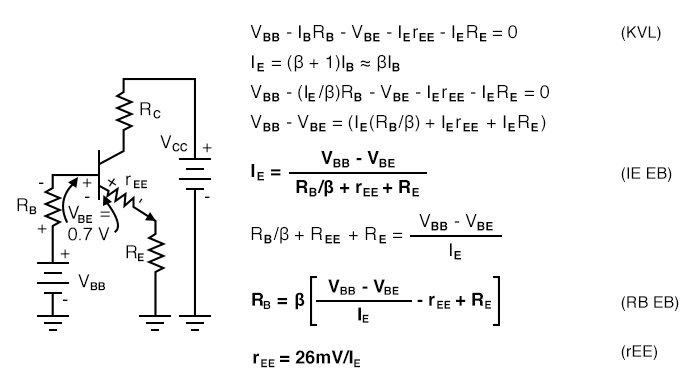
Emitter-bias equations with internal emitter resistance rEE included.

The more accurate emitter-bias equations in the figure above may be derived by writing a KVL equation. Alternatively, start with equations IE emitter-bias and RB emitter-bias in Figure previous, substituting RE with rEE+RE. The result is equations IE EB and RB EB, respectively in Figure above.

Redo the RB calculation in the previous example emitter-bias with the inclusion of rEE and compare the results.

The inclusion of rEE in the calculation results in a lower value of the base resistor RB as shown in Table below. It falls below the standard value 82k resistor instead of above it.

Effect of inclusion of rEE on calculated RB

Bypass Capacitor for RE

One problem with emitter bias is that a considerable part of the output signal is dropped across the emitter resistor RE (figure below). This voltage drop across the emitter resistor is in series with the base and of opposite polarity compared with the input signal. (This is similar to a common collector configuration having <1 gain.) This degeneration severely reduces the gain from base to collector. The solution for AC signal amplifiers is to bypass the emitter resistor with a capacitor. This restores the AC gain since the capacitor is short for AC signals. The DC emitter current still experiences degeneration in the emitter resistor, thus, stabilizing the DC current.

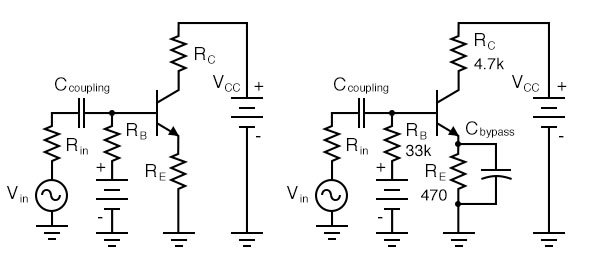
Cbypass is required to prevent AC gain reduction.

The value of the bypass capacitor depends on the lowest frequency to be amplified.

For radio frequencies Cbpass would be small. For an audio amplifier extending down to 20Hz it will be large. A “rule of thumb” for the bypass capacitor is that the reactance should be 1/10 of the emitter resistance or less. The capacitor should be designed to accommodate the lowest frequency being amplified. The capacitor for an audio amplifier covering 20Hz to 20kHz would be:

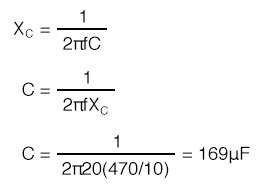
Note that the internal emitter resistance rEE is not bypassed by the bypass capacitor.

Voltage Divider Bias

Stable emitter bias requires a low voltage base bias supply, the figure below. The alternative to a base supply VBB is a voltage divider based on the collector supply VCC.

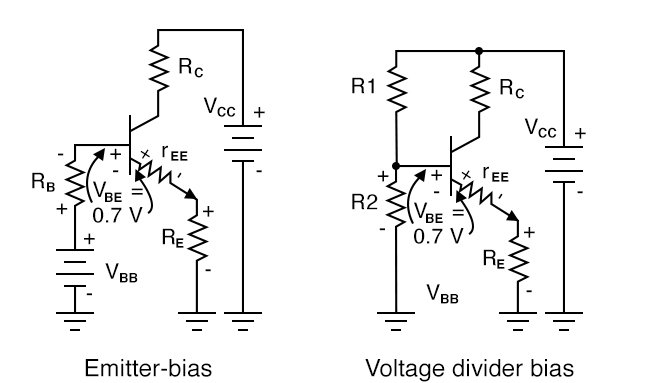
Voltage Divider bias replaces base battery with voltage divider.

The design technique is to first work out an emitter-bias design, Then convert it to the voltage divider bias configuration by using Thevenin’s Theorem. [TK1] The steps are shown graphically in the figure below. Draw the voltage divider without assigning values. Break the divider loose from the base. (The base of the transistor is the load.) Apply Thevenin’s Theorem to yield a single Thevenin equivalent resistance Rth and voltage source Vth.

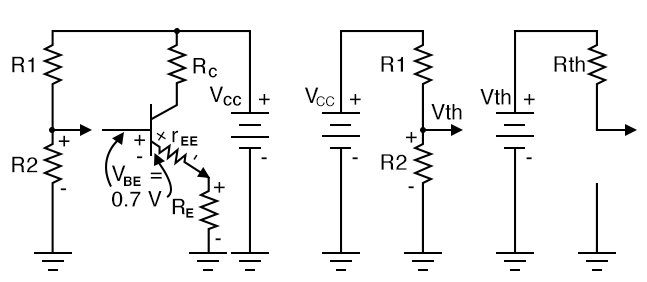
Thevenin’s Theorem converts voltage divider to single supply Vth and resistance Rth.

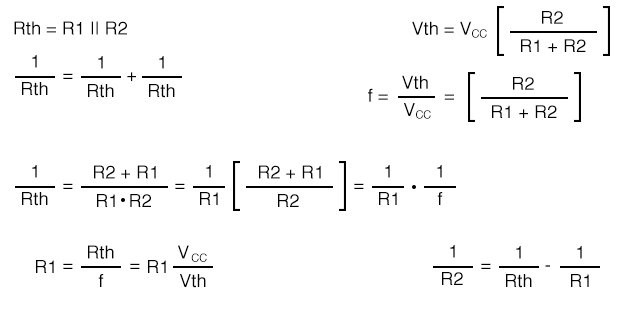
The Thevenin equivalent resistance is the resistance from load point (arrow) with the battery (VCC) reduced to 0 (ground). In other words, R1||R2. The Thevenin equivalent voltage is the open-circuit voltage (load removed). This calculation is by the voltage divider ratio method. R1 is obtained by eliminating R2 from the pair of equations for Rth and Vth. The equation of R1 is in terms of known quantities Rth, Vth, Vcc. Note that Rth is RB, the bias resistor from the emitter-bias design. The equation for R2 is in terms of R1 and Rth.

Convert this previous emitter-bias example to voltage divider bias.

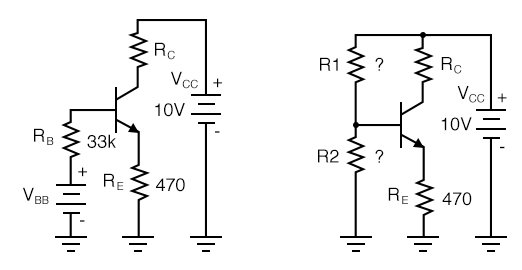
Emitter-bias example converted to voltage divider bias.

These values were previously selected or calculated for an emitter-bias example

Substituting VCC , VBB , RB yields R1 and R2 for the voltage divider bias configuration.

R1 is a standard value of 220K. The closest standard value for R2 corresponding to 38.8k is 39k. This does not change IE enough for us to calculate it. Example Problems 1. Calculate the bias resistors for the cascode amplifier in the figure below. VB2 is the bias voltage for the common-emitter stage. VB1 is a fairly high voltage at 11.5 because we want the common-base stage to hold the emitter at 11.5-0.7=10.8V, about 11V. (It will be 10V after accounting for the voltage drop across RB1 .) That is, the common-base stage is the load, substitute for a resistor, for the common-emitter stage’s collector. We desire a 1mA emitter current.

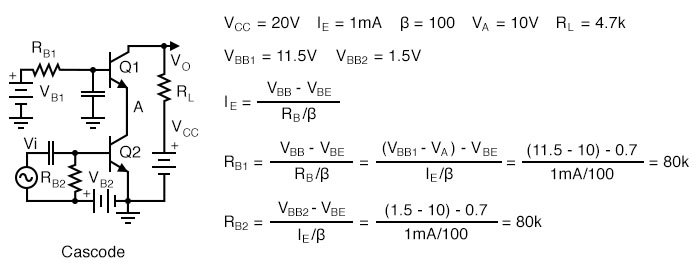
Bias for a cascode amplifier.

2. Convert the base bias resistors for the cascode amplifier to voltage divider bias resistors driven by the VCC of 20V.

The final circuit diagram is shown in the “Practical Analog Circuits” chapter, “Class A cascode amplifier . . . ” cascode, Ch 9 .