Amplifier frequency response

Amplifier frequency response

INTRODUCTION

$Description: C:\Users\User\Downloads\elecrical circute\23_files\image001.png$

As such for any electronic circuit, the behavior of amplifiers is affected by the frequency of the signal on their input terminal. This characteristic is known as the frequency response.

Frequency response is one of the most important property of amplifiers. In the frequency range that amplifiers have been designed for, they must deliver a constant and acceptable level of gain. The frequency response depends directly on the components and the architecture chosen for the design of the amplifier.

In this tutorial, we will focus on this important feature of amplifiers. First of all, the notion of frequency response is detailed along with some basic related concepts and we will present how to quantify it. In the second section, we will understand which component affects the frequency response and how. In the rest of the article a method to establish the low and high frequency responses is presented. These results will finally be synthesized in the conclusion to plot the global frequency response of a Common Emitter Amplifier.

DEFINITIONS

Before defining in details the frequency response, we need to present the unit of decibel (dB) and the logarithmic scale related to it. When studying the frequency response, it is indeed more suitable to convert either the power or voltage gain into dB and to represent the frequency scale in a logarithmic (log) scale.

If we consider an amplifier with power gain AP and voltage gain AV, the power and voltage gain in dB are defined by :

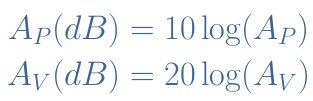
$Description: C:\Users\User\Downloads\elecrical circute\23_files\image002.png$

eq 1 : Power and voltage gain in dB

While the gains in linear scale are always positive (AP,AV≥0), their equivalent in dB can either be positive if an amplification is being realized (AP,AV>1) or negative if the input signal is attenuated (AP,AV<1).

Often, it is not the gain AV(dB) that is investigated but rather a normalized ratio AV/AV,mid(dB)=20log(AV/AV,mid). Where AV,mid is called the midrange gain and represents the maximum gain of the amplifier in its frequency working range, for example 20 Hz – 20 kHz for an audio amplifier.

Therefore, when AV=AV,mid, the normalized gain (written indifferently AV) is AV(dB)=0. This sets a 0 dB reference when the gain is maximum. It is important to note that when the power is divided by two, we observe that AP(dB)=10log(0.5)=-3 dB.

The frequency at which the power drops to 50 % of its midrange value is known as the cutoff frequency and noted fc. Each time that the power is halved, a reduction of 3 dB of the normalized gain is observed. Therefore AP=-3 dB corresponds to AV,mid/2, AP=-6 dB corresponds to AV,mid/4 and so on …

For this same frequency, the voltage (or current) is multiplied by a factor √2=0.7. Halving the voltage signal corresponds to a reduction of 6 dB and follows the same pattern as presented for the power gain.

The most common tool used to represent the frequency response of any system is the Bode plot. It consists of the normalized gain AV(dB) as a function of the frequency in log scale. A simplified Bode graph of an amplifier is shown in the Figure 1 below :

$Description: C:\Users\User\Downloads\elecrical circute\23_files\image003.png$

fig 1 : Typical Bode graph of an amplifier

The light blue curve is called the asymptotic representation while the dark blue curve is the real frequency response of the circuit.

In Figure 1, two different cutoff frequencies can be distinguished : flc for “low cutoff” and fhc for “high cutoff”. The quantity fhc-flc is called the bandwidth and represents the frequency range where the gain is above the -3 dB plateau.

One last observation can be given about the slope of the frequency response out of the bandwidth. First of all, they are not necessary identical for low and high frequencies. Moreover, as we will see later, the slope has a value that depends on the reactance of the components that induce a dependency with the frequency.

EFFECT OF THE CAPACITORS

Let’s consider a Common Emitter Amplifier (CEA) which configuration is shown in Figure 2 :

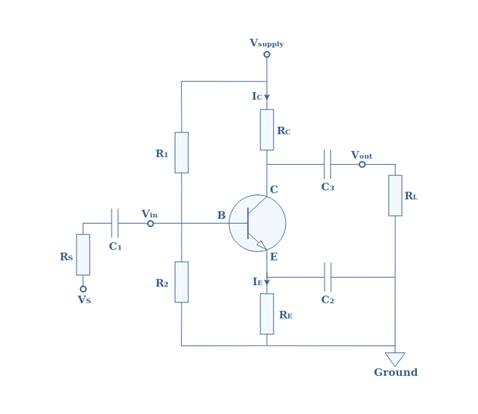
$Description: C:\Users\User\Downloads\elecrical circute\23_files\image004.jpg$

fig 2 : Common Emitter Amplifier

The structure around the BJT transistor consists of a voltage divider network (R1 and R2), a load (RL), coupling capacitors (C1 and C3) and a bypass capacitor C2.

What is important to keep in mind is that capacitors have a property called reactance that is an equivalent of the resistance. The reactance (XC) of capacitors depends on the frequency and the value of the capacitor, it satisfies the following formula :

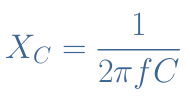
$Description: C:\Users\User\Downloads\elecrical circute\23_files\image005.png$

eq 2 : Reactance of capacitors

Independently of the value of the capacitor, when the frequency is low, XC tends to be high. Near DC signals, capacitors behave therefore as open circuits. On the other hand, when the frequency increases XC tends to zero and capacitors act as short circuits.

At low input frequencies, the coupling capacitors will more likely block the signal, since XC1 and XC3 are higher, more voltage drop will be observed across C1 and C3. This results in a lower voltage gain.

At high input frequencies the bypass capacitor C2 shortens the emitter branch to the ground and the voltage gain of the amplifier is AV=(RC//RL)/re with re being the small diode emitter resistance. When the frequencies are lower, the resistance between the emitter and the ground is no longer only re but RE+re and therefore the voltage gain decreases to AV=(RC//RL)/(RE+re).

There is another type of capacitors that affect the frequency response of the amplifier and is not represented in Figure 2. They are known as internal transistor capacitors and represented in Figure 3 below :

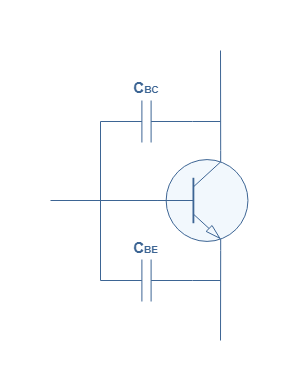
$Description: C:\Users\User\Downloads\elecrical circute\23_files\image006.png$

fig 3 : Internal transistor capacitors

Whereas the coupling and bypass capacitors act as high-pass filter (they block low frequencies), these internal capacitors behave differently. Indeed, if the frequency is low, CBC and CBE act as an open circuit and the transistor is not affected at all. However, if the frequency increases, more signal passes through them instead of going in the base branch of the transistor, therefore decreasing the voltage gain.

A very important formula is given in Equation 3 and links the cutoff frequency of a RC filter :

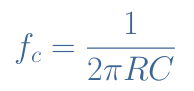
$Description: C:\Users\User\Downloads\elecrical circute\23_files\image007.png$

eq 3 : Cutoff frequency of a RC filter

LOW FREQUENCY RESPONSE

Having all of this information in mind, let’s calculate and plot the low frequency response of the CEA of Figure 2 with the below given parameters :

$Description: C:\Users\User\Downloads\elecrical circute\23_files\image008.png$

One last thing we need to understand before plotting the Bode graph is about the slope out of the midrange values. The decrease of A_V,mid with the frequency is called roll-off and its value for each simple RC filter is -20 dB/decade (dB/dec). This value means for high-pass filters (resp. low-pass filters) that each time the frequency is divided by 10 (resp. multiplied by 10), a decrease of -20 dB is observed for the gain of the amplifier.

When multiple filters are blocking the same range of frequencies, the roll-off is enhanced. In our example three filters are simultaneously blocking the frequencies below 35 Hz, the roll-off is therefore 3*(-20 dB/dec)=-60 dB/dec.

This information can be synthesized in a Bode plot showing the low frequency response of the CEA in asymptotic representation :

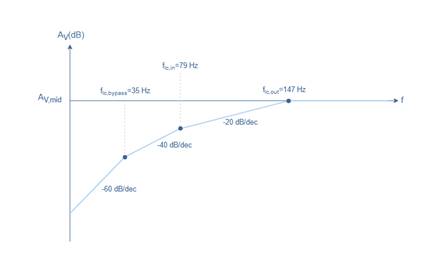
$Description: C:\Users\User\Downloads\elecrical circute\23_files\image009.jpg$

fig 4 : Low frequency response of the CEA