COMBINATIONAL GATES

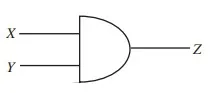
Yet another representation of boolean functions makes use of the combinational gate abstraction. We will see how gates are built out of primitive lumped circuit elements in Chapter 6. For now, let us focus on the gate-level abstraction. The digital gate notation for the boolean equation Z = X AND Y is shown in Figure

The AND gate

The output of combinational gates is purely a function of their inputs. Therefore, combinational functions can always be enumerated using truth tables. Combinational gates follow the static discipline. Provided they are given inputs that fall within valid input levels, they will produce outputs that satisfy valid output thresholds.

Combinational gate abstraction

A combinational gate is an abstract representation of a circuit that satisfies two properties:

1. Its outputs are a function of its inputs alone.

2. It satisfies the static discipline.

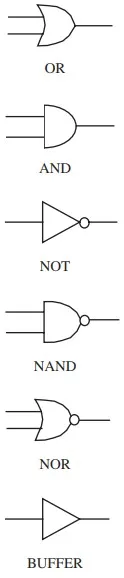
Figure  shows several useful gate symbols. We have already seen the gate-level representation of the AND function. The OR gate performs the OR function of its inputs. The NOT gate takes the complement of its input. For convenience, we often denote the NOT function in logic circuits using the ‘‘◦’’ symbol. The buffer gate or identity gate simply copies the input value to its output, that is, A = A. Its use will become apparent in Section 6.9.2. The NAND function is equivalent to the AND operation followed by the NOT operation. For example, A = B NAND C is equivalent to A = B AND C. It is also equivalent to the statement: A is FALSE only if both B and C are TRUE. Similarly, the NOR operation is equivalent to the OR operation followed by the NOT operation