BOOLEAN LOGIC

The binary representation has a natural correspondence to logic, and therefore digital circuits are commonly used to implement logic procedures. For example, consider the logical ‘‘if’’ statement:

If X is TRUE AND Y is TRUE then Z is TRUE else Z is FALSE

We can represent this statement using a boolean equation as:

Z = X AND Y

In the previous equation, Z is true only when both X and Y are TRUE and FALSE otherwise. For brevity we often represent the AND function using the ‘‘·’’ symbol as:

Z = X · Y

Just as we represent the algebraic expression X × Y as xy, we often drop the AND symbol and write:

Z = X · Y = XY

The boolean equation for the statement:

If (A is TRUE) OR (B is NOT TRUE) then (C is TRUE) else (C is FALSE) is C = A + .

The preceding equation contains two other useful functions. The OR function is represented using ‘‘+’’ and the NOT function using the bar symbol as in ‘‘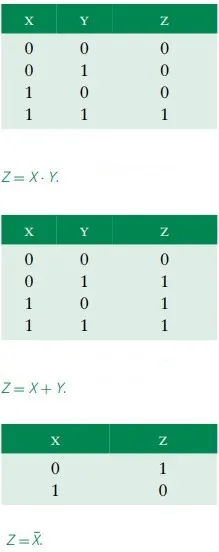’’ or the ∼ symbol as in ∼ X. For example, we represent the condition ‘‘B is FALSE’’ as 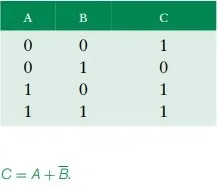or ∼ B. We call 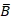the complement of B. The logic operators that we have seen thus far are summarized in Table. For convenience, we will use 1, TRUE, and high interchangeably. Similarly, we will use 0, FALSE, and low interchangeably.