BATTERIES

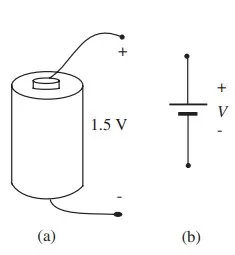
Cell phone batteries, laptop batteries, flashlight batteries, watch batteries, car batteries, calculator batteries, are all common devices in our culture. All are sources of energy, derived in each case from an internal chemical reaction. The important specifications for a battery are its nominal voltage, its total store of energy, and its internal resistance. In this section, we will assume that the internal resistance of a battery is zero. The voltage measured at the terminals of a single cell is fundamentally related to the chemical reaction releasing the energy. In a flashlight battery, for example, the carbon central rod is approximately 1.5 V positive with respect to the zinc case, as noted in Figure a.

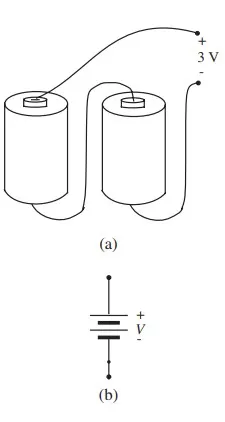
In a circuit diagram, such a single-cell battery is usually represented schematically by the symbol shown in Figure b. Of course, to obtain a larger voltage, several cells can be connected in series: the positive terminal of the first cell connected to the negative terminal of the second cell, and so forth, as suggested pictorially in Figure 1.10. Multiple-cell batteries are usually represented by the symbol in Figure 1.10b, (with no particular correspondence between the number of lines and the actual number of cells in series)

The second important parameter of a battery is the total amount of energy it can store, often measured in joules. However, if you pick up a camcorder or flashlight battery, you might notice the ratings of ampere-hours or watt-hours. Let us reconcile these ratings. When a battery is connected across a resistive load in a circuit, it delivers power. The lightbulb in Figure a is an example of a resistive load.

The power delivered by the battery is the product of the voltage and the current: p = VI

Power is delivered by the battery when the current I flowing out of the positive voltage terminal of the battery is positive. Power is measured in watts. A battery delivers one watt of power when V is one volt and I is one ampere. Power is the rate of delivery of energy. Thus the amount of energy w delivered by the battery is the time integral of the power

If a constant amount of power p is delivered over an interval T, the energy w supplied is w = pT.

The battery delivers one joule of energy if it supplies one watt of power over one second. Thus, joules and watt-seconds are equivalent units. Similarly if a battery delivers one watt for an hour, then we say that it has supplied one watt-hour (3600 joules) of energy. Assuming that the battery terminal voltage is constant at V, because the power delivered by the battery is the product of the voltage and the current, an equivalent indication of the power delivered is the amount of current being supplied. Similarly, the product of current and the length of time the battery will sustain that current is an indication of the energy capacity of the battery

When a battery is connected across a resistor, as illustrated in Figure 1.4, we saw that the battery delivers energy at some rate. The power was the rate of delivery of energy. Where does this energy go? Energy is dissipated by the resistor, through heat, and sometimes even light and sound if the resistor overheats and explodes!

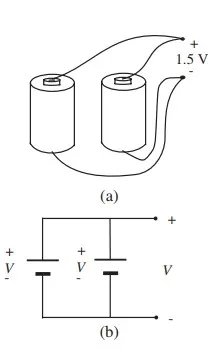
If one wishes to increase the current capacity of a battery without increasing the voltage at the terminals, individual cells can be connected in parallel, as shown in Figure  It is important that cells to be connected in parallel be nearly identical in voltage to prevent one cell from destroying another. For example, a 2-V lead-acid cell connected in parallel with a 1.5 V flashlight cell will surely destroy the flashlight cell by driving a huge current through it. The corresponding constraint for cells connected in series is that the nominal current capacity be nearly the same for all cells. The total energy stored in a multicell battery is the same for series, parallel, or series-parallel interconnections