Generators

Generators are in load flow analysis modelled as current injections, see Figure 2.12. In steady state a generator is commonly controlled so that the active power injected into the bus and the voltage at the generator terminals are kept constant. This will be elaborated later when formulating the load flow equations. Active power from the generator is determined by the turbine control and must of course be within the capability of the turbinegenerator system. Voltage is primarily determined by the reactive power injection into the node, and since the generator must operate within its reactive capability curve it is not possible to control the voltage outside certain limits. The reactive capability of a generator depends on a number of quantities, such as active power, bus voltage and other operating conditions, and a typical example is shown in Figure 2.13. The shape of the generator capability curve is specific for each generator and depends on design characteristics, type of generator, hydro or steam turbine, stability constraints, etc.

Stator Current Heating Limit

The losses in the armature windings are given by RtI 2 t , with obvious notation. These losses result in a temperature rise in the armature windings, and this must be limited to a given value otherwise the generator is damaged or its life time is reduced. Since the complex power is given by S = P + jQ = UtI ∗ t it means that for a given terminal voltage, Ut , circles in the P − Q-plane with centre at the origin correspond to constant value of the magnitude of the armature current It . The stator current limit for a given terminal voltage is thus a circle with the centre at the origin. At high

Model of a generator connected to bus k.

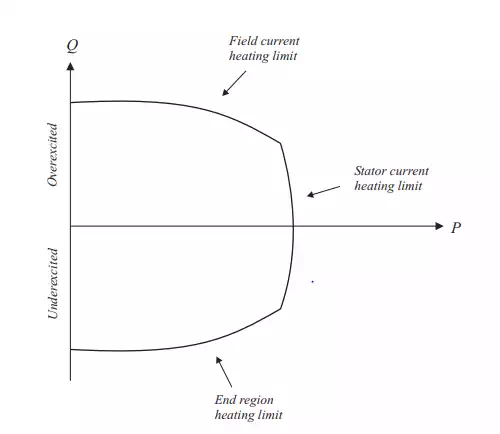
Reactive capability curve of a turbo generator

loading of the generator, this is usually determining the reactive capability of the synchronous machine.

Field Current Heating

 Limit The reactive power that can be generated at low load is determined by the field current heating limit. It can be shown that the locus for constant field current is a circle with the centre on the Q-axis at −E2 t /Xs, where Et is the terminal voltage and Xs is the synchronous reactance. The radius is given by machine parameters and typical behaviour is shown in Figure 2.13. The field current heating is usually limiting at overexcited operation at low load.

Stator End Region Heating Limit

When the synchronous machine is underexcited the armature end leakage flux is increased. This flux enters and leaves in a direction perpendicular to the stator laminations causing eddy currents in the laminations, and hence heating. This can limit the capability, particularly for round rotor machines. A typical example of such a limitation is shown in Figure 2.13. The limits on reactive power generation and absorption given in this subsection and the two previous ones are imposed by internal synchronous machine design. As seen they are dependent on the terminal voltage of the generator. There are also other considerations that can further limit the reactive capability of the synchronous machine. These are stability limits that could further limit the operation of the machine in underexcited operation.