Basic Power Flow Problem

T HE POWER FLOW PROBLEM can be formulated as a set of nonlinear algebraic equality/inequality constraints. These constraints represent both Kirchhoff’s laws and network operation limits. In the basic formulation of the power flow problem, four variables are associated to each bus (network node) k:

Basic Bus Types

Equality and Inequality Constraints

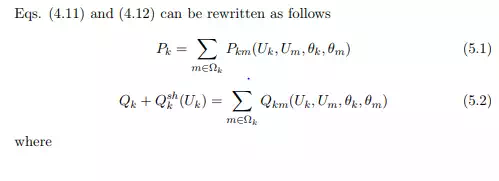
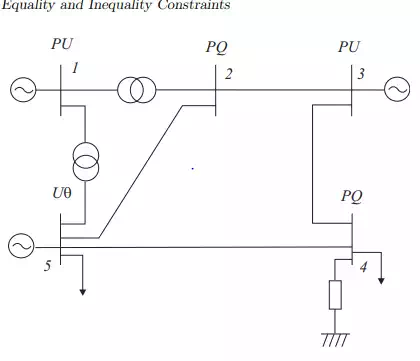
5-bus system

When no inequality constraints are violated, nothing is affected in the power flow equations, but if a limit is violated, the bus status is changed and it is enforced as an equality constraint at the limiting value. This normally requires a change in bus type: if, for example, a Q limit of a PU bus is violated, the bus is transformed into an PQ bus (Q is specified and the U becomes a problem unknown). A similar procedure is adopted for backing-off when ever appropriate. What is crucial is that bus type changes must not affect solvability. Various other types of limits are also considered in practical implementations, including branch current flows, branch power flows, active power generation levels, transformer taps, phase shifter angles, and area interchanges.

Problem Solvability