Solution of Electric Circuit Based on Node Voltage Method
In the node voltage
method, we identify all the nodes on the circuit. Choosing one of them as the
reference voltage (i.e., zero potential) and subsequently assign other node
voltages (unknown) with respect to a reference voltage (usually ground voltage
taken as zero (0) potential and denoted by ![]() If the circuit has “n”
nodes there are “n-1” node voltages are unknown (since we are always free to
assign one node to zero or ground potential). At each of these “n-1” nodes, we
can apply KCL equation. The unknown node voltages become the independent
variables of the problem and the solution of node voltages can be obtained by
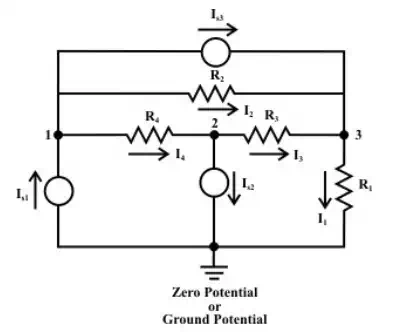
solving a set of simultaneous equations. Let us consider a simple dc network as
shown in Figure to find the currents through different branches using “Node
voltage” method.
If the circuit has “n”
nodes there are “n-1” node voltages are unknown (since we are always free to
assign one node to zero or ground potential). At each of these “n-1” nodes, we
can apply KCL equation. The unknown node voltages become the independent
variables of the problem and the solution of node voltages can be obtained by
solving a set of simultaneous equations. Let us consider a simple dc network as
shown in Figure to find the currents through different branches using “Node
voltage” method.
![]()
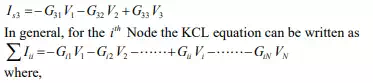

Step-1:
Identify all nodes in the circuit. Select one node as the reference node (assign as ground potential or zero potential) and label the remaining nodes as unknown node voltages with respect to the reference node.
Step-2:
Assign branch currents in each branch. (The choice of direction is arbitrary).
Step-3:
Express the branch currents in terms of node assigned voltages.
Step-4:
Write the standard form of node equations by inspecting the circuit. (No of node equations = No of nodes (N) – 1).
Step-5:
Solve a set of simultaneous algebraic equation for node voltages and ultimately the branch currents.
Remarks:
· Sometimes it is convenient to select the reference node at the bottom of a circuit or the node that has the largest number of branches connected to it.
· One usually makes a choice between a mesh and a node equations based on the least number of required equations
Example: Find the value of the current I flowing through the battery using ‘Node voltage’ method.
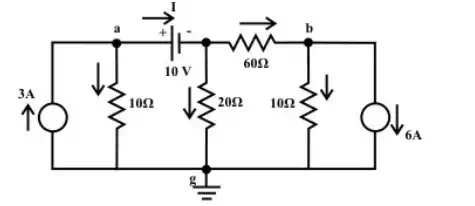
Solution:
All nodes are indicated
in fig and ‘Node-g’ is selected as reference voltage. If a voltage source is
connected directly between the two nodes, the current flowing through the
voltage source cannot be determined directly since the source voltage (Vs) is
independent of current. Further to note that the source voltage (Vs)fixes the
voltage between the nodes only. For the present example, the voltage of the
central node is known since it is equal to ![]()
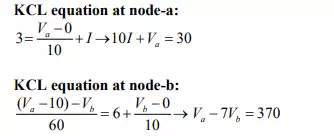
To solve the equations,
we need one more equation which can be obtained by applying KCL at the central
node (note central node voltage is ![]() .
.
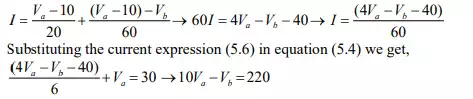
Equations
can be solved to find ![]()
We can now refer to original circuit to find directly the voltage across every element and the current through every element. The value of current flowing through the voltage source can be computed using the equation and it is given by I =1.307 A . Note that the current I (+ve) is entering through the positive terminal of the voltage source and this indicates that the voltage source is absorbing the power, in other words this situation is observed when charging a battery or source.