Phasor representation of Voltage and Current

The voltage and current waveforms are given as

It can be seen from the waveforms (Fig b) of the two sinusoidal quantities – voltage and current, that the voltage, V lags the current I, which means that the positive maximum value of the voltage is reached earlier by an angle, φ , as compared to the positive maximum value of the current. In phasor notation as described earlier, the voltage and current are represented by OP and OQ (Fig a) respectively, the length of which are proportional to voltage, V and current, I in different scales as applicable to each one. The voltage phasor, OP (V) lags the current phasor, OQ (I) by the angle φ , as two phasors rotate in the anticlockwise direction as stated earlier, whereas the angle φ is also measured in the anticlockwise direction. In other words, the current phasor (I) leads the voltage phasor (V).

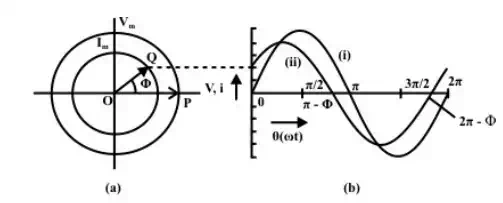
(a) Phasor representation of a sinusoidal (i) voltage and (ii) current and (b) Waveform

Of the two terms in each phasor, the first one is termed as real or its component in x-axis, while the second one is imaginary or its component in y-axis, as shown in Fig a. The angle, φ is in degree or rad.

Phasor Algebra

Before discussing the mathematical operations, like addition/subtraction and multiplication/division, involving phasors and also complex quantities, let us take a look at the two forms – polar and rectangular, by which a phasor or complex quantity is represented. It may be observed here that phasors are also taken as complex, as given above.

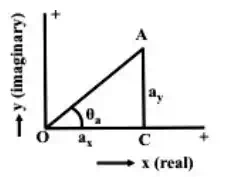
Representation of a phasor , both in rectangular and polar forms

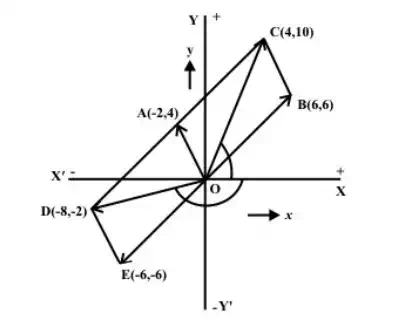
Addition and subtraction of two phasors represented in polar form , as an example

Firstly, let us take the addition and subtraction of the above two phasors. The sum and

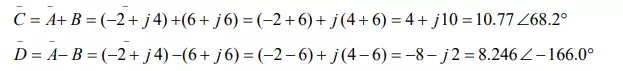
It may be noted that for the addition and subtraction operations involving phasors, they should be represented in rectangular form as given above. If any one of the phasors is in polar form, it should be transformed into rectangular form, for calculating the results as shown. If the two phasors are both in polar form, the phasor diagram (the diagram must be drawn to scale), or the geometrical method can be used as shown in Fig. The result obtained using the diagram, as shown are the same as obtained earlier.

Now, the multiplication and division operations are performed, using the above two phasors represented in polar form. If any one of the phasors is in rectangular form, it may be transformed into polar form. Also note that the same symbols for the phasors are used here, as was used earlier. Later, the method of both multiplication and division using rectangular form of the phasor representation will be explained.

The above result can be calculated by the procedure described earlier, using the rectangular form of the two phasors as

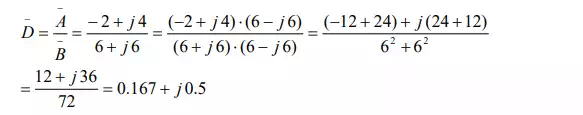
The procedure for the elementary operations using two phasors only, in both forms of representation is shown. It can be easily extended, for say, addition/multiplication, using three or more phasors. The simplification procedure with the scalar quantities, using the different elementary operations, which is well known, can be extended to the phasor quantities. This will be used in the study of ac circuits to be discussed in the following lessons.

The background required, i.e. phasor representation of sinusoidal quantities (voltage/current), and algebra – mathematical operations, such as addition/subtraction and multiplication/division of phasors or complex quantities, including transformation of phasor from rectangular to polar form, and vice versa, has been discussed here. The study of ac circuits, starting from series ones, will be described in the next few lessons.

Representation of a phasor and Transformation

A phasor or a complex quantity in rectangular form is,

where  are real and imaginary parts, of the phasor respectively. In polar form, it is expressed as

where A and θ a are magnitude and phase angle of the phasor. From the two equations or expressions, the procedure or rule of transformation from polar to rectangular form is

From the above, the rule for transformation from rectangular to polar form is

The examples using numerical values are given at the end of this lesson.