Periodic Voltage or Current Waveform
Average value The current waveform shown in Fig a, is periodic in nature, with time period, T. It is positive for first half cycle, while it is negative for second half cycle.
The average value of the waveform, i(t) is defined as
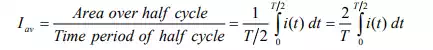
Please note that, in this case, only half cycle, or half of the time period, is to be used for computing the average value, as the average value of the waveform over full cycle is zero (0).
If the half time period (T/2) is divided into 6 equal time intervals (ΔT ),
![]()
Please note that no. of time intervals is n = 6.
Root Mean Square (RMS) value
For this current in half time period subdivided into 6-time intervals as given above, in the resistance R, the average value of energy dissipated is given by
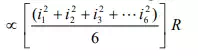
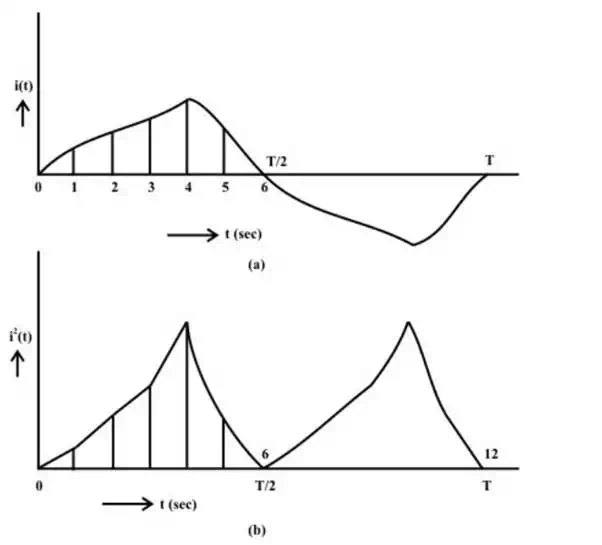
Periodic current waveform (a) current (i) (b) square of current (i^2)
The graph of the square of the current waveform, i^2 (t) is shown in Fig.b. Let I be the value of the direct current that produces the same energy dissipated in the resistance R, as produced by the periodic waveform with half time period subdivided into time intervals,
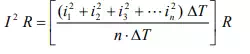
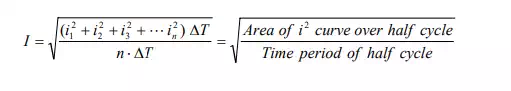
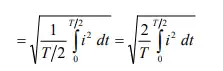
This value is termed as Root Mean Square (RMS) or effective one. Also to be noted that the same rms value of the current is obtained using the full cycle, or the time period.
Average and RMS Values of Sinusoidal Voltage Waveform
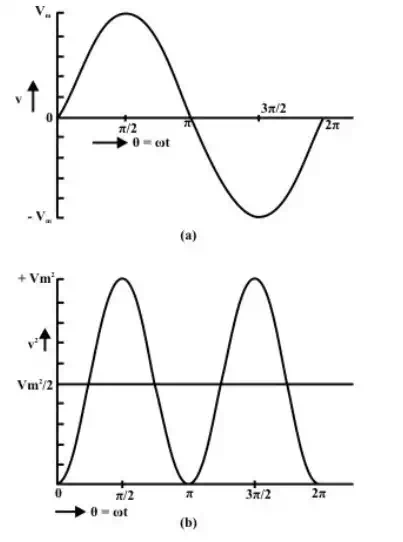
Sinusoidal voltage waveform (a) voltage (b) Square of voltage (v^2)
As shown earlier, normally the voltage generated, which is also transmitted and then distributed to the consumer, is the sinusoidal waveform with a frequency of 50 Hz in this country. The waveform of the voltage v(t), and the square of waveform, v^2(t), are shown in figures a and b respectively.

If the average value of the above waveform is computed over total time period T, it comes out as zero, as the area of first (positive) half cycle is the same as that of second (negative) half cycle. However, the rms value remains same, if it is computed over total time period.
The different factors are defined as:
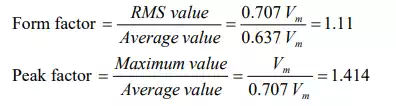
Note:
The rms value is always greater than the average value, except for a rectangular waveform, in which case the heating effect remains constant, so that the average and the rms values are same.