Response of a series R-L-C circuit due to a dc voltage source

Consider a series R - L – C circuit as shown in fig, and it is excited with a dc voltage source . Applying KVL around the closed path for t >0 ,

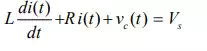
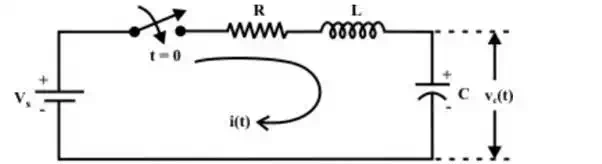
A simple R-L-C circuit excited with a dc voltage source

The current through the capacitor can be written as

Substituting the current ‘i (t)’expression in eq.(11.1) and rearranging the terms,

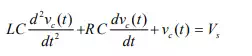
The above equation is a 2nd-order linear differential equation and the parameters associated with the differential equation are constant with time. The complete solution of the above differential equation has two components; the transient response  and the steady state response . Mathematically, one can write the complete solution as

Since the system is linear, the nature of steady state response is same as that of forcing function (input voltage) and it is given by a constant value A . Now, the first part  of the total response is completely dies out with time while  and it is defined as a transient or natural response of the system. The natural or transient response of second order differential equation can be obtained from the homogeneous equation (i.e., from force free system) that is expressed by

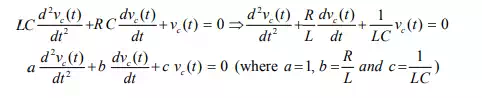
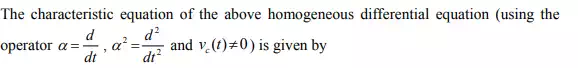
and solving the roots of this equation one can find the constants α1 and α of the exponential terms that associated with transient part of the complete solution and they are given below.

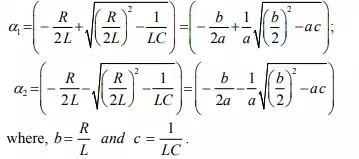
The roots of the characteristic equation are classified in three groups depending upon the values of the parameters R,  L and C of the circuit.

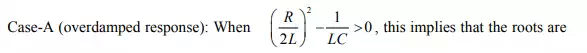
distinct with negative real parts. Under this situation, the natural or transient part of the complete solution is written as

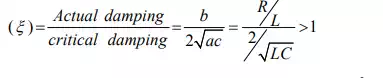
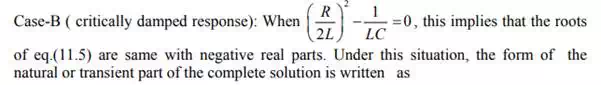
where the natural or transient response is a sum of two terms: a negative exponential and a negative exponential multiplied by a linear term. The expression that arises from the natural solution of second order differential equation having the roots of characteristic equation are same value can be verified following the procedure given below.

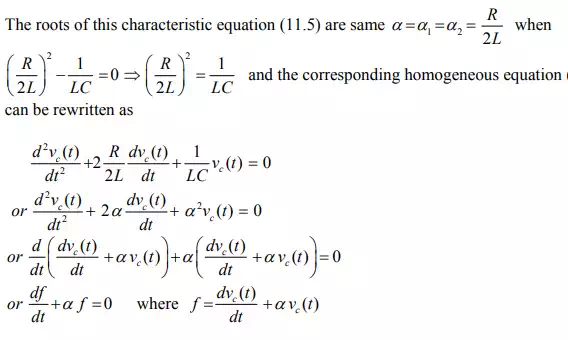
easily verify above statements by adopting the concept of maximization problem of a single valued function. The second order system results the speediest response possible without any overshoot while the roots of characteristic equation of system having the same negative real parts. The response of such a second order system is defined as a critically damped system’s response. In this case damping ratio.

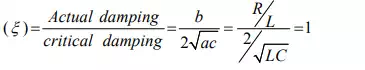
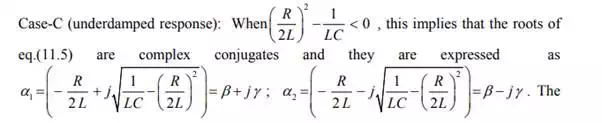
form of the natural or transient part of the complete solution is written as

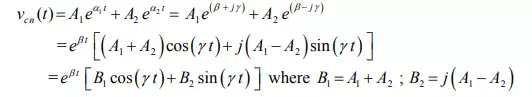
conjugates. The equation further can be simplified in the following form:

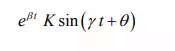
calculated using the initial conditions of the circuit. The system response exhibits oscillation around the steady state value when the roots of characteristic equation are complex and results an under-damped system’s response. This oscillation will die down with time if the roots are with negative real parts. In this case the damping ratio

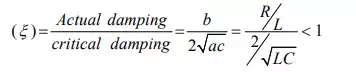
Finally, the response of a second order system when excited with a dc voltage source is presented in fig  for different cases, i.e., (i) under-damped (ii) over-damped (iii) critically damped system response

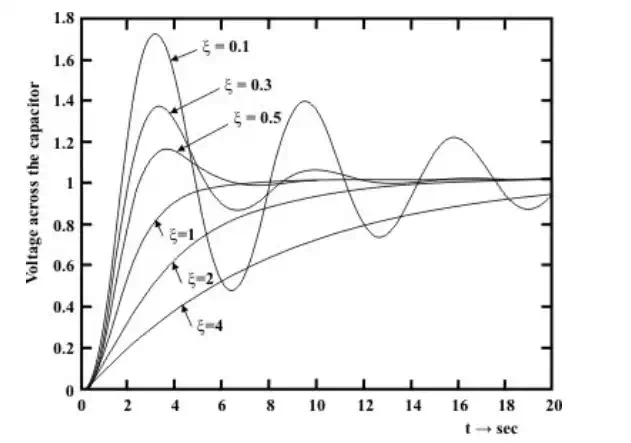
System response for series R-L-C circuit

(a) Underdamped

(b) Critically damped

Overdamped system