Maximum Power Transfer Theorem

In an electric circuit, the load receives electric energy via the supply sources and converts that energy into a useful form. The maximum allowable power receives by the load is always limited either by the heating effect (in case of resistive load) or by the other power conversion taking place in the load. The Thevenin and Norton models imply that the internal circuits within the source will necessarily dissipate some of power generated by the source. A logical question will arise in mind, how much power can be transferred to the load from the source under the most practical conditions? In other words, what is the value of load resistance that will absorbs the maximum power from the source? This is an important issue in many practical problems and it is discussed with a suitable example.

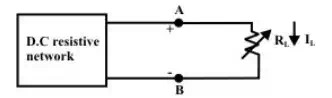
                                        (a)

Let us consider an electric network as shown in fig.8.6(a), the problem is to find the choice of the resistance RL so that the network delivers maximum power to the load or in other words what value of load resistance RL will absorb the maximum amount of power from the network. This problem can be solved using nodal or mesh current analysis to obtain an expression for the power absorbed by RL , then the derivative of this expression with respect to RL will establish the condition under what circumstances the maximum power transfer occurs. The effort required for such an approach can be quite tedious and complex. Fortunately, the network shown in fig.(a) can be represented by an equivalent Thevenin’s voltage source as shown in fig.(b).

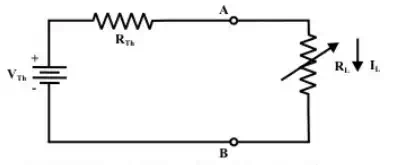
               (b) the circuit for maximum power transfer

In fig.(b) a variable load resistance RL is connected to an equivalent Thevenin circuit of original circuit(fig.(a)). The current for any value of load resistance is

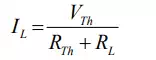
Then, the power delivered to the load is

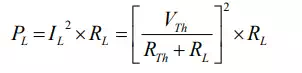
The load power depends on both and  ; however,  is constant for the equivalent Thevenin network. So power delivered by the equivalent Thevenin network to the load resistor is entirely depends on the value of . To find the value of  that absorbs a maximum power from the Thevenin circuit, we differentiate  with respect to

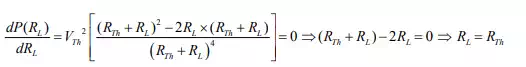
For maximum power dissipation in the load, the condition given below must be satisfied

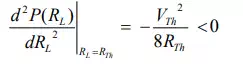
This result is known as “Matching the load” or maximum power transfer occurs when the load resistance  matches the Thevenin’s resistance of a given systems. Also, notice that under the condition of maximum power transfer, the load voltage is, by voltage division, one-half of the Thevenin voltage. The expression for maximum power dissipated to the load resistance is given by

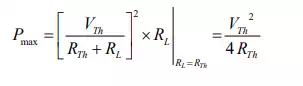
The total power delivered by the source

This means that the Thevenin voltage source itself dissipates as much power in its internal resistance  as the power absorbed by the load . Efficiency under maximum power transfer condition is given by

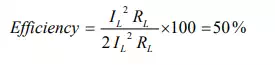
delivered to the load varies as shown in fig.

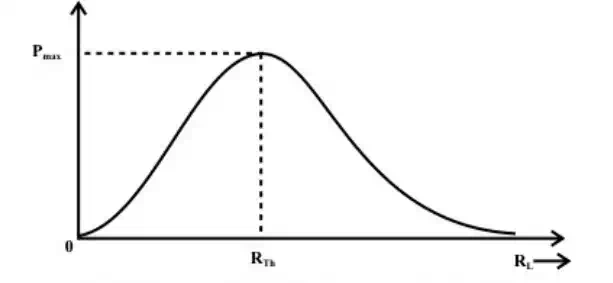
(c) power dissipated to the load as a function of  load resistance