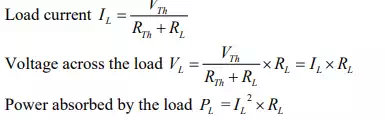The procedure for applying Thevenin’s theorem

To find a current  through the load resistance  (as shown in fig.(a)) using Thevenin’s theorem, the following steps are followed:

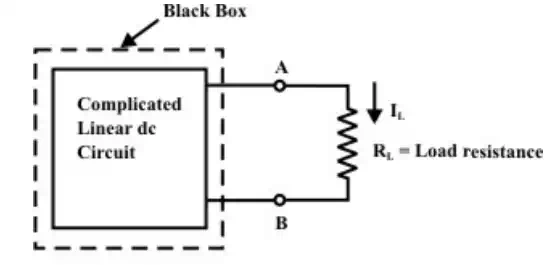
(a)

Step-1: Disconnect the load resistance  from the circuit, as indicated in fig.(b).

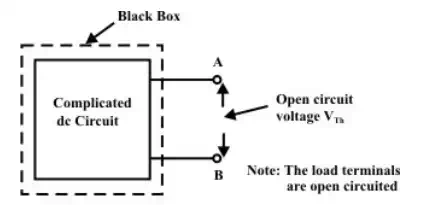
(b)

Step-2: Calculate the open-circuit voltage (shown in fig.8.2(b)) at the load terminals (A& B ) after disconnecting the load resistance . In general, one can apply any of the techniques (mesh-current, node-voltage and superposition method) learnt in earlier lessons to compute (experimentally just measure the voltage across the load terminals using a voltmeter).

Step-3: Redraw the circuit (fig.(b)) with each practical source replaced by its internal resistance as shown in fig(c). (note, voltage sources should be short-circuited (just remove them and replace with plain wire) and current sources should be open-circuited (just removed).

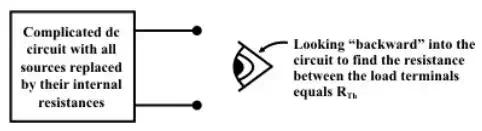
                   (c)

Step-4: Look backward into the resulting circuit from the load terminals ( A& B ) , as suggested by the eye in fig.(c). Calculate the resistance that would exist between the load terminals ( or equivalently one can think as if a voltage source is applied across the load terminals and then trace the current distribution through the circuit (fig.(c)) in order to calculate the resistance across the load terminals.) The resistance is described in the statement of Thevenin’s theorem. Once again, calculating this resistance may be a difficult task but one can try to use the standard circuit reduction technique or Y −Δ or Δ−Y transformation techniques.

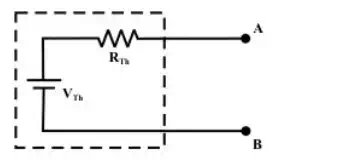
(d) Dash-portion of the circuit (a) is equivalently replaced by a practical voltage source

Step-5: Place  in series with to form the Thevenin’s equivalent circuit (replacing the imaginary fencing portion or fixed part of the circuit with an equivalent practical voltage source) as shown in fig.(d).

Step-6: Reconnect the original load to the Thevenin voltage circuit as shown in fig.(e); the load’s voltage, current and power may be calculated by a simple arithmetic operation only.

                           (e)