Superposition Theorem in the context of dc voltage and current sources acting in a resistive network

Statement of superposition theorem

In any linear bilateral network containing two or more independent sources (voltage or current sources or combination of voltage and current sources ), the resultant current / voltage in any branch is the algebraic sum of currents / voltages caused by each independent sources acting along, with all other independent sources being replaced meanwhile by their respective internal resistances.

Superposition theorem can be explained through a simple resistive network as shown in fig. and it has two independent practical voltage sources and one practical current source.

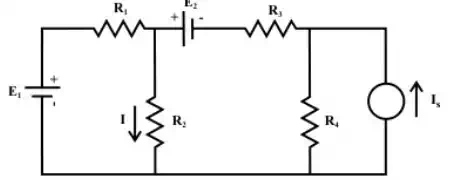
One may consider the resistances R1 and R3 are the internal resistances of the voltage sources whereas the resistance R4 is considered as internal resistance of the current source. The problem is to determine the response I in the in the resistor R2 . The current I can be obtained from

according to the application of the superposition theorem. It may be noted that each independent source is considered at a time while all other sources are turned off or killed. To kill a voltage source means the voltage source is replaced by its internal resistance

 whereas to kill a current source means to replace the current source by its internal resistance

Remarks:

Superposition theorem is most often used when it is necessary to determine the individual contribution of each source to a particular response.

Procedure for using the superposition theorem

Step-1: Retain one source at a time in the circuit and replace all other sources with their internal resistances.

Step-2: Determine the output (current or voltage) due to the single source acting alone using the techniques discussed in lessons 3 and 4.

Step-3: Repeat steps 1 and 2 for each of the other independent sources.

Step-4: Find the total contribution by adding algebraically all the contributions due to the independent sources.