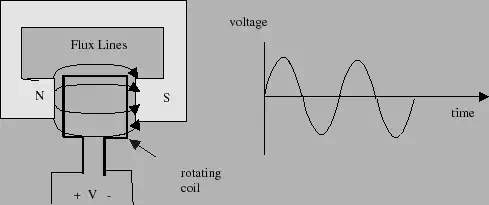
Faraday's law of induction provides a basis for converting mechanical energy into electrical energy. The basic idea is to move a coil of wire relative to a magnetic field. This motion will generate a current in the wire. Such a device is called a generator and a conceptual drawing of this device is shown in figure 1.

$Description: Description: \begin{figure}\epsfxsize =5.in \epsfclipon \centerline{\epsffile{fig-lab8/generator.eps}} \end{figure}$

Figure 1: A generator and the voltage it generates

To make things simple, the coil is usually made to rotate within the field. As the coil rotates, it cuts through the flux lines, generating a voltage across the coil's terminals. When the face of the coil is parallel to the field, it cuts rapidly through the flux lines. But when the coil has turned 90 degrees and is perpendicular to the field lines, then the motion of the coil is tangential to the field and no voltage is produced. As the coil turns past this point, it cuts through the field in the opposite direction, generating a negative voltage. The end result of this chain of events is that the voltage produced by the generator varies as the cosine of the angle as shown below. This sinusoidal waveform is referred to as an alternating current or AC.

The equation for a waveform of this type is:

$Description: Description: $\displaystyle v(t) = A \cos(\omega t + \phi)$$

(1)

where is the amplitude, $Description: Description: $\omega$$ is the frequency, and $Description: Description: $\phi$$ is the phase . Since is a time-varying voltage signal, has units of volts. The frequency has units of radians per second. Phase is measured in radians. We often measure frequency in a related unit of cycles per second. A cycle corresponds to $Description: Description: $2 \pi$$ radians.

The sinusoidal waveform in equation 1 is a periodic waveform. A signal is periodic if and only if there exists such that for all . To see if a sinusoidal waveform is periodic we therefore need to find such that

$Description: Description: $\displaystyle A \cos(\omega t + \phi) = A \cos(\omega (t+T) + \phi)$$

(2)

In particular, we know that the cosine function repeats every $Description: Description: $2 \pi$$ radians so we need to find such that

$Description: Description: $\displaystyle A \cos(\omega(t+T)+\phi) = A \cos(\omega t + 2 \pi + \phi)$$

(3)

Clearly this occurs if $Description: Description: $\omega T = 2 \pi$$ or rather

$Description: Description: $\displaystyle T = \frac{2 \pi}{\omega}$$

(4)

is the fundamental period of this sinusoidal function. The size of a sine wave can be measured in a variety of ways. We may, for instance, use the waveform's amplitude () to specify the waveform's size. Another measure of "size" is the signal's root mean square or rms strength

$Description: Description: $\displaystyle \mbox{RMS} = \left[ \int_{0}^{\omega/2 \pi} \left( A \cos(\omega t + \phi) \right)^2 dt \right]^{1/2}$$

(5)

Since generators naturally produce sine waves, these waveforms play an important role in electrical engineering. It also turns out that sine waves also provide an efficient way of transporting electrical energy over a long distance. This is part of the reason why AC voltages are used in international power grids and, of course, this is why your wall socket provides a 120 volts (rms) AC voltage at 60 Hz. In contrast to AC voltages, batteries provide a direct current or DC voltage. DC voltages are constant over time. In order to obtain DC voltages from an AC wall socket we're going to have to find some way of regulating the AC power source.

What is Alternating Current (AC)?

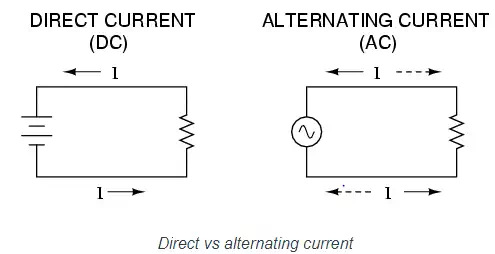
Most students of electricity begin their study with what is known as direct current (DC), which is electricity flowing in a constant direction, and/or possessing a voltage with constant polarity. DC is the kind of electricity made by a battery (with definite positive and negative terminals), or the kind of charge generated by rubbing certain types of materials against each other.

Alternating Current vs Direct Current

As useful and as easy to understand as DC is, it is not the only “kind” of electricity in use. Certain sources of electricity (most notably, rotary electro-mechanical generators) naturally produce voltages alternating in polarity, reversing positive and negative over time. Either as a voltage switching polarity or as a current switching direction back and forth, this “kind” of electricity is known as Alternating Current (AC): Figurebelow

Whereas the familiar battery symbol is used as a generic symbol for any DC voltage source, the circle with the wavy line inside is the generic symbol for any AC voltage source. One might wonder why anyone would bother with such a thing as AC. It is true that in some cases AC holds no practical advantage over DC. In applications where electricity is used to dissipate energy in the form of heat, the polarity or direction of current is irrelevant, so long as there is enough voltage and current to the load to produce the desired heat (power dissipation). However, with AC it is possible to build electric generators, motors, and power distribution systems that are far more efficient than DC, and so we find AC used predominately across the world in high power applications. To explain the details of why this is so, a bit of background knowledge about AC is necessary.

AC Alternators

f a machine is constructed to rotate a magnetic field around a set of stationary wire coils with the turning of a shaft, AC voltage will be produced across the wire coils as that shaft is rotated, in accordance with Faraday’s Law of electromagnetic induction. This is the basic operating principle of an AC generator, also known as an alternator:

Notice how the polarity of the voltage across the wire coils reverses as the opposite poles of the rotating magnet pass by. Connected to a load, this reversing voltage polarity will create a reversing current direction in the circuit. The faster the alternator’s shaft is turned, the faster the magnet will spin, resulting in an alternating voltage and current that switches directions more often in a given amount of time. While DC generators work on the same general principle of electromagnetic induction, their construction is not as simple as their AC counterparts. With a DC generator, the coil of wire is mounted in the shaft where the magnet is on the AC alternator, and electrical connections are made to this spinning coil via stationary carbon “brushes” contacting copper strips on the rotating shaft. All this is necessary to switch the coil’s changing output polarity to the external circuit so the external circuit sees a constant polarity: Figure below

The generator shown above will produce two pulses of voltage per revolution of the shaft, both pulses in the same direction (polarity). In order for a DC generator to produce constant voltage, rather than brief pulses of voltage once every 1/2 revolution, there are multiple sets of coils making intermittent contact with the brushes. The diagram shown above is a bit more simplified than what you would see in real life. The problems involved with making and breaking electrical contact with a moving coil should be obvious (sparking and heat), especially if the shaft of the generator is revolving at high speed. If the atmosphere surrounding the machine contains flammable or explosive vapors, the practical problems of spark-producing brush contacts are even greater. An AC generator (alternator) does not require brushes and commutators to work, and so is immune to these problems experienced by DC generators.

AC Motors

The benefits of AC over DC with regard to generator design is also reflected in electric motors. While DC motors require the use of brushes to make electrical contact with moving coils of wire, AC motors do not. In fact, AC and DC motor designs are very similar to their generator counterparts (identical for the sake of this tutorial), the AC motor being dependent upon the reversing magnetic field produced by alternating current through its stationary coils of wire to rotate the rotating magnet around on its shaft, and the DC motor being dependent on the brush contacts making and breaking connections to reverse current through the rotating coil every 1/2 rotation (180 degrees).

Transformers

So we know that AC generators and AC motors tend to be simpler than DC generators and DC motors. This relative simplicity translates into greater reliability and lower cost of manufacture. But what else is AC good for? Surely there must be more to it than design details of generators and motors! Indeed there is. There is an effect of electromagnetism known as mutual induction, whereby two or more coils of wire placed so that the changing magnetic field created by one induces a voltage in the other. If we have two mutually inductive coils and we energize one coil with AC, we will create an AC voltage in the other coil. When used as such, this device is known as a transformer: Figure below

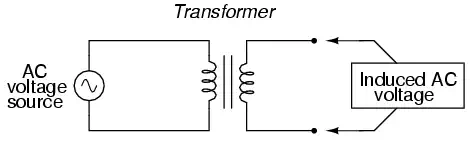
Description: Description: https://sub.allaboutcircuits.com/images/02004.webp
Transformer “transforms” AC voltage and current.

The fundamental significance of a transformer is its ability to step voltage up or down from the powered coil to the unpowered coil. The AC voltage induced in the unpowered (“secondary”) coil is equal to the AC voltage across the powered (“primary”) coil multiplied by the ratio of secondary coil turns to primary coil turns. If the secondary coil is powering a load, the current through the secondary coil is just the opposite: primary coil current multiplied by the ratio of primary to secondary turns. This relationship has a very close mechanical analogy, using torque and speed to represent voltage and current, respectively: Figure below

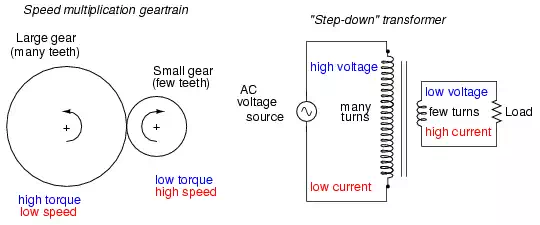
Description: Description: https://sub.allaboutcircuits.com/images/02005.webp
Speed multiplication gear train steps torque down and speed up. Step-down transformer steps voltage down and current up.

If the winding ratio is reversed so that the primary coil has less turns than the secondary coil, the transformer “steps up” the voltage from the source level to a higher level at the load: Figure below

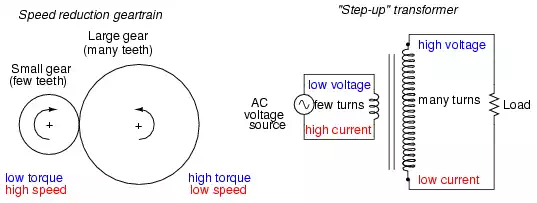
Description: Description: https://sub.allaboutcircuits.com/images/02006.webp
Speed reduction gear train steps torque up and speed down. Step-up transformer steps voltage up and current down.

The transformer’s ability to step AC voltage up or down with ease gives AC an advantage unmatched by DC in the realm of power distribution in figure below. When transmitting electrical power over long distances, it is far more efficient to do so with stepped-up voltages and stepped-down currents (smaller-diameter wire with less resistive power losses), then step the voltage back down and the current back up for industry, business, or consumer use.

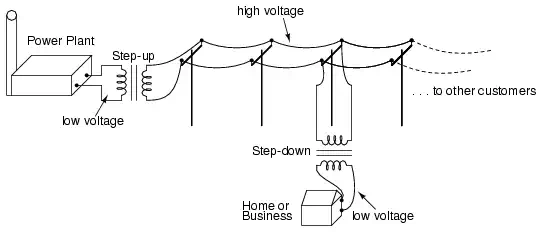
Description: Description: https://sub.allaboutcircuits.com/images/02007.webp
Transformers enable efficient long distance high voltage transmission of electric energy.

Transformer technology has made long-range electric power distribution practical. Without the ability to efficiently step voltage up and down, it would be cost-prohibitive to construct power systems for anything but close-range (within a few miles at most) use. As useful as transformers are, they only work with AC, not DC. Because the phenomenon of mutual inductance relies on changing magnetic fields, and direct current (DC) can only produce steady magnetic fields, transformers simply will not work with direct current. Of course, direct current may be interrupted (pulsed) through the primary winding of a transformer to create a changing magnetic field (as is done in automotive ignition systems to produce high-voltage spark plug power from a low-voltage DC battery), but pulsed DC is not that different from AC. Perhaps more than any other reason, this is why AC finds such widespread application in power systems.