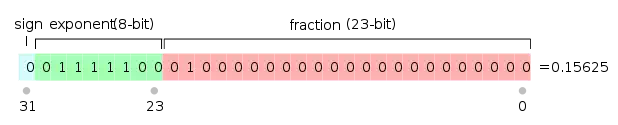numerical methods

numerical methods

The term “numerical method” usually refers to a way of computing something that is usually symbolic using numbers. For example, consider the problem of computing a derivative:

$\frac{d}{d x} f (x) where f (x) = x^{2}$

If we were just doing math on paper we would compute this via one of the techniques from intro calculus and get

$\frac{d}{d x} f (x) = 2 x$

A simple case like this could be solved by a computer symbolically (the way that we just solved it). However, it is often easier (and possibly computationally cheaper) to compute the derivative a different way (numerically), especially if the derivative is harder than $x^{2}$

So what would a numerical solution look like?

Remember from intro calculus that before they taught you the derivative tricks like $\frac{d}{d x} x^{n} = n x^{n - 1}$ your teacher should’ve mentioned the definition of a derivative:

$\frac{d}{d x} f (x) = l i m_{h \to 0} \frac{f (x + h) - f (x)}{h}$ (x)=limh→0f(x+h)−f(x)h

One way to compute a derivative would be to replace $h a s h \to 0$ $h a s h$ → 0 with a very small value of $h$ (say $10^{- 5}$ ). This would give you a value almost equal to the derivative. That’s a very simple numerical method. In essence numerical methods are ways of approximating solutions to mathematical problems using numerical values rather than symbolic values.

Introduction to Numerical Methods

Mathematical models are a central piece of science and engineering. Some models have closed-form solutions, therefore they can be solved analytically. Many models can not be solved analytically or the analytic solution is too costly to be practical. All models can be solved computationally and the result may not be the exact answer but it can be useful. George E. P. Box was right by saying All models are wrong, but some are useful. Since errors are inevitable a more practical question we ought to ask is how close the answer needs to be for it to be useful. In lots of engineering situations the only way to get the "right answer" is to use the following formula:

right answer = wrong answer + corrections

Rounding Off Errors

earning objectives:

· recognize the sources of overflow and underflow errors

· convert between decimal representation and floating point representation

· understand the IEEE 754 standard of a floating point representation on computers

· calculate the machine epsilon of a representation.

Integer Overflow (Error)[edit]

How are integers represented on a computer?

Most computers use the 2's complement representation. Assume we have 4 bits to store and operate on an integer we may end up with the following situation:

0111 (7)

+0001 (1)

-----

1000 (-8)

The numbers in parentheses are the decimal value represented by the 2's complement binary integers. The result is obviously wrong because adding positive numbers should never result in a negative number. The reason for the error is that result exceeds the range of values the 4-bit can store with the 2's complement notation.

The following example gives the wrong answer for the same reason. The leading 1 can not be stored.

1000 (-8)

+1111 (-1)

-----

10111 (7)

Floating-point Underflow (Error)[edit]

In math numbers have infinite precision, but numerals (representations of number) have finite precision. One third (1/3) can not be represented precisely in decimal or it would require a infinite number of digits, which is impossible. Similarly 0.2 can not be represented precisely in binary, which means its binary representation is not precise (an approximation). When numbers are computed/calculated on a computer, the representations of the numbers are being manipulated and the result will very likely be imprecise. This is an important limitation of computing. Essentially the computer must be considered a part of our model when we solve problems computationally. We must factor the computer in because it is a binary computer approximating base ten numbers. An floating-point underflow or underflow happens when the result of a calculation is too small to be stored. A underflow can be caused by the (negative) overflow of the exponent.

What is the binary representation {\displaystyle 11.1875_{10}}

Fixed-point Representation[edit]

Any real number can be represented in binary as a fixed-point number. To convert the number from its decimal (base 10) representation to its binary representation we need to convert the integer part and the fractional part to binary separately, because different methods are required. Please check out the following resource on how to do that [1].

Floating-point Representation[edit]

Given a fixed number of digits we can represent a larger range of values using the floating-point format. The IEEE 754 format is a international standard on floating-point representation of numbers in computers. A 32-bit floating point number (single precision) is represented using three parts as shown in the figure: : a sign bit, a (biased) exponent, and a fraction.

The value represented by an IEEE 754 single precision floating point number can be calculated using the following formula:

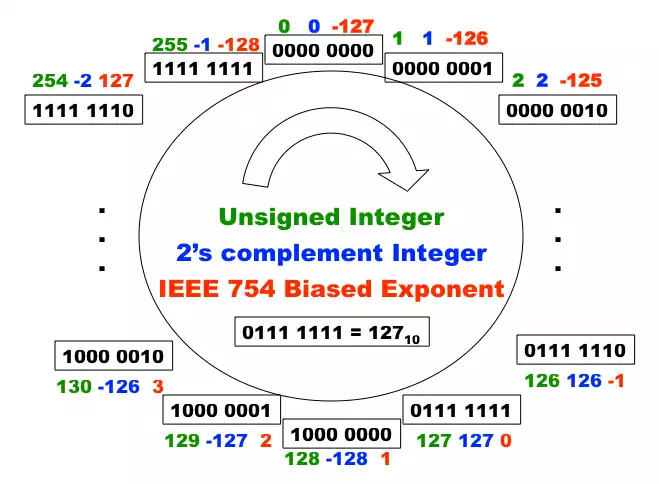
For example to store in IEEE single precision floating point format , we need to store a sign bit of $0$ (0 means positive and 1 means negative), a fraction of $.01$ , and a biased exponent of . Because all numbers, except 0, will have a leading one in the binary "scientific" representation that one is not stored in IEEE 754 format to save one bit. We will say how the value 0 is represented in a moment. The biased exponent is just a clever way to use the available bits to represent more values and make number comparison faster. We will use 8-bit exponent as an example. In the figure above, we have 8-bit which can represent $2^{8}=256_{10}$ different things. The bit patterns have no intrinsic meaning, so we can use them to represent anything we want. The green part shows the values those bit patterns represent when they are treated as binary representations of unsigned integers. The problem is that we want to represent negative values as well. One easy solution is to treat the left most bit as the sign bit: 0 means positive and 1 means negative, which result in two zeros $+0$ and $-0$ . The blue part shows what happens when we use the 2's complement scheme to represent both positive and negative values using the same set of bit patterns. Recall that the 2's complement scheme is often used to simply hardware design so that we can use addition to do subtraction: a - b is the same as a + (the 2's complement of -b). To get the 2's complement of a positive integer is to invert all the bits and add 1 to it. Now any subtraction can be done with a inversion and two additions. The problem with 2's complement representation is that a "larger" looking pattern does not necessarily represent a larger value.

The red part shows the biased exponent represented by the same set of bit patterns. As you can see a "larger" looking pattern always represent a larger value except for the all one patterns, which is used to represent a special value. The advantage of the biased exponent representation is that each value is represented by a unique pattern (no two zeros) and comparing floating point numbers is easier. The exponent is put before the fraction in IEEE 754 standard so that floating point numbers can be compared by treating their bit patterns as unsigned integers (much faster).

The following table shows some special values represented by special bit patterns.

biased expoent	fraction	numbers
00...00	0	0
00...00	nonzero	denormalized
11...11	0	+/- infinity
11...11	nonzero	NaN (Not a Number)

Because the implicit/hidden 1 is always added to the fraction to get the represented value a special pattern is needed to represent the zero value. Now the result of a division by zero can be represented as +/- infinity (division by zero in integer operation will crash your program). ${\sqrt {-4}}$ , and $0/0$ can be represented as NaN, which helps debugging your programs.

What is the IEEE 754 floating-point representation of this number: $-2.340625\times 10^{1}$

What is the decimal equivalent of this IEEE 754 floating-point number: 1100 0000 1111 0000 0000 0000 0000 0000?

What is the largest IEEE 754 single precision floating-point number?

What are the downsides of floating-point or scientific representation? With five digits we can represent $999.99_{10}$ precisely using fixed point notation. However, when we use the following scientific/floating-point notation $n.nn\times 10^{nn}$ the closest value we can represent is $9.99\times 10^{02}$ and the error is $999.99-999=0.99$ - a loss of precision.