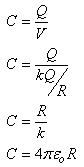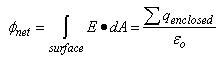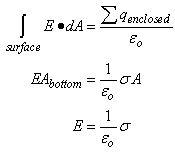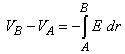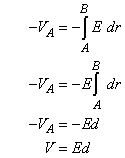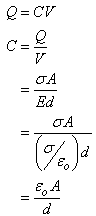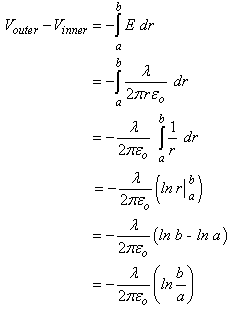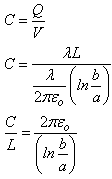Spherical, Parallel Plate, and Cylindrical Capacitors

Spherical Capacitors

Consider an isolated, initially uncharged, metal conductor. After the first small amount of charge, q, is placed on the conductor, its voltage becomes  as compared to V = 0 at infinity. To further charge the conductor, work must be done to bring increments of charge, dq, to its surface:

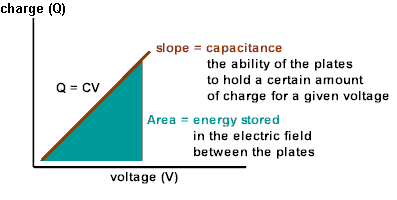
The amount of work required to bring in each additional charged-increment, dq, increases as the spherical conductor becomes more highly charged. The total electric potential energy of the conductor can be calculated by

The capacitance of the spherical conductor can be calculated as

Notice that a spherical conductor's capacitance is totally dependent on the sphere's radius.

Parallel Plate Capacitors

Since we know that the basic relationship Q = CV, we must obtain expressions for Q and V to evaluate C.

Using Gauss' Law,

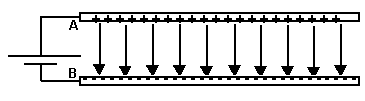
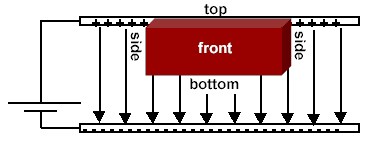
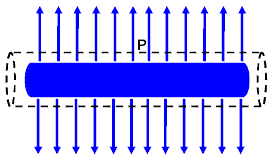
We can evaluate E, the electric field between the plates, once we employ an appropriate gaussian surface. In this case, we will use a box with one side embedded within the top plate.

This box has six faces: a top, a bottom, left side, right side, front surface and back surface. Since the top surface is embedded within the metal plate, no field lines will pass through it since under electrostatic conditions there are no field lines within a conductor. Field lines will only run parallel to the area vector of the bottom surface. They will be perpendicular to the area vectors of the other four sides. Thus,

The total charge enclosed in our gaussian box equals

Thus,

We also know that the potential difference across the plates is equal to

Since plate B is defined to be at V = 0,

we can rewrite this as

Substituting into Q = CV yields

To relate the energy per unit volume stored in a capacitor to the magnitude of its electric field, we will build on our relationship for the energy stored in a capacitor developed in a previous lesson.

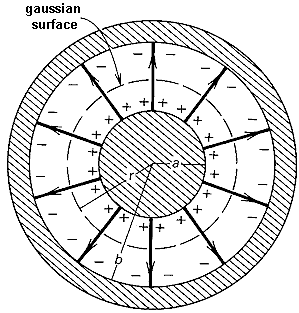
Cylindrical Capacitors

 Now let's consider the geometry of a cylindrical capacitor. Suppose that our capacitor is composed of an inner cylinder with radius a enclosed by an outer cylinder with radius b.

Since we know that the basic relationship Q = CV, we must obtain expressions for Q and V to evaluate C.

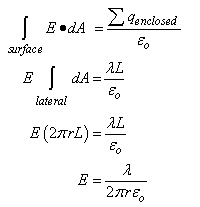
 Again, we will use Gauss' Law to evaluate the electric field between the plates by using a gaussian surface that is cylindrical in shape and of length L. The cylinder has a uniform charge per unit length of .

We also know that the potential difference across the cylinders is equal to

Since the outer plate is negative, its voltage can be set equal to 0, and we can state that the potential difference across the capacitors equals

Returning to Q = CV

This represents the capacitance per unit length of our cylindrical capacitor. An excellent example of a cylindrical capacitor is the coaxial cable used in cable TV systems.