Relationship between Binary - Octal and Binary-hexadecimal

As demonstrated by the table bellow, there is a direct correspondence between the binary system and the octal system, with three binary digits corresponding to one octal digit. Likewise, four binary digits translate directly into one hexadecimal digit.

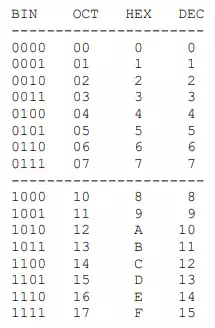
With such relationship, In order to convert a binary number to octal, we partition the base 2 number into groups of three starting from the radix point, and pad the outermost groups with 0’s as needed to form triples. Then, we convert each triple to the octal equivalent.

For conversion from base 2 to base 16, we use groups of four.

Consider converting 10110₂ to base 8:

10110₂ = 010₂ 110₂ = 2₈ 6₈ = 26₈

Notice that the leftmost two bits are padded with a 0 on the left in order to create a full triplet.

10110110₂ = 1011₂ 0110₂ = B₁₆ 6₁₆ = B6₁₆

(Note that ‘B’ is a base 16 digit corresponding to 1110. B is not a variable.) The conversion methods can be used to convert a number from any base to any other base, but it may not be very intuitive to convert something like 513.03 to base 7. As an aid in performing an unnatural conversion, we can convert to the more familiar base 10 form as an intermediate step, and then continue the conversion from base 10 to the target base. As a general rule, we use the polynomial method when converting into base 10, and we use the remainder and multiplication methods when converting out of base 10.