Convert From Any Base to Decimal

Let's think more carefully what a decimal number means. For example, 1234 means that there are four boxes (digits); and there are 4 one's in the right-most box (least significant digit), 3 ten's in the next box, 2 hundred's in the next box, and finally 1 thousand's in the left-most box (most significant digit). The total is 1234:

Thus, each digit has a value: 10^0 =1 for the least significant digit, increasing to 10^{^1} =10, 10^{^2} =100, 10^{^3} =1000, and so forth.

Likewise, the least significant digit in a hexadecimal number has a value of 16^0 =1 for the least significant digit, increasing to 16^{^1} =16 for the next digit, 16^{^2} =256 for the next, 16^{^3} =4096 for the next, and so forth. Thus, 1234 means that there are four boxes (digits); and there are 4 one's in the right-most box (least significant digit), 3 sixteen's in the next box, 2 256's in the next, and 1 4096's in the left-most box (most significant digit). The total is:

1*4096 + 2*256 + 3*16 + 4*1 = 4660

In summary, the conversion from any base to base 10 can be obtained from the formulae

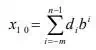
Where b is the base, di the digit at position i, m the number of digit after the decimal point, n the number of digits of the integer part and X₁₀ is the obtained number in decimal. This form the basic of the polynomial method of converting numbers from any base to decimal

Example. Convert 234.14 expressed in an octal notation to decimal.

2*8² + 3*8¹ + 4*8⁰ +1*8^-1 + 4*8^-2 = 2*64 +3*8 +4*1 +1/8 +4/64 =156.1875

Example. Convert the hexadecimal number 4B3 to decimal notation. What about the decimal equivalent of the hexadecimal number 4B3.3?