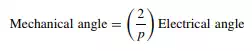No-Load Operation
When the ideal machine is connected to an infinite bus, a three-phase balanced voltage (V1) is applied to the stator winding (within the context of this work, three-phase systems and machines are assumed). As described above, it can be shown that a three-phase balanced voltage applied to a three-phase winding evenly distributed around the core of an armature will produce a rotating (revolving) magneto-motive force (mmf) of constant magnitude (Fs). This mmf, acting upon the reluctance encountered along its path, results in the magnetic flux (φs) previously introduced. The speed at which this field revolves around the center of the machine is related to the supply frequency and the number of poles, by the following expression:
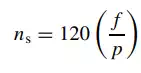
where
f = electrical frequency in Hz
p = number of poles of the machine
ns = speed of the revolving field in revolutions per minute (rpm)
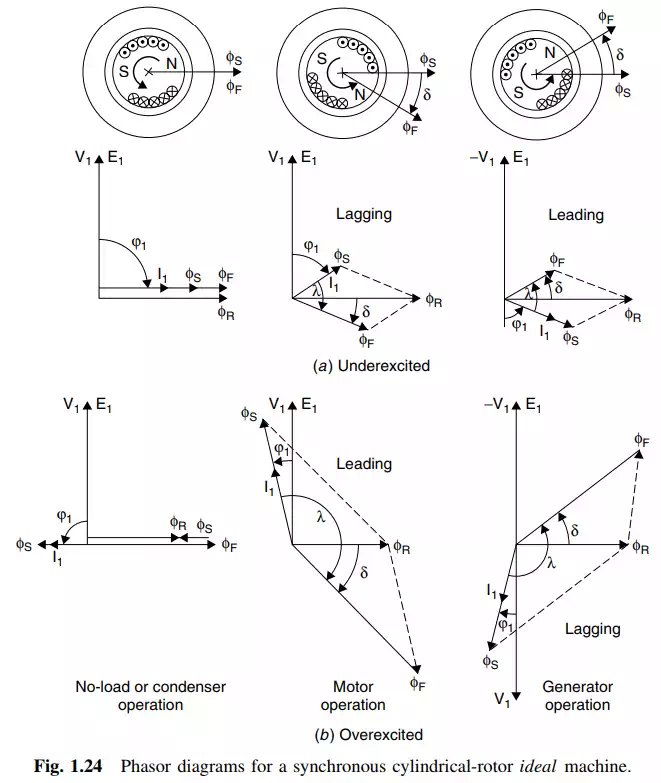
If no current is supplied to the dc field winding, no torque is generated, and the resultant flux (φr), which in this case equals the stator flux (φs), magnetizes the core to the extent the applied voltage (V1) is exactly opposed by a counterelectromotive force (cemf) (E1). If the rotorís excitation is slightly increased, and no torque is applied to the shaft, the rotor provides some of the excitation required to produce (E1), causing an equivalent reduction of (φs). This situation represents the underexcited condition shown in condition no load (a) in Figure 1.24. When operating under this condition, the machine is said to behave as a lagging condenser, meanings it absorbs reactive power from the network. If the field excitation is increased over the value required to produce (E1), the stator currents generate a flux that counteracts the field-generated flux. Under this condition, the machine is said to be overexcited, shown as condition no load (b) in Figure 1.24. The machine is behaving as a leading condenser; that is, it is delivering reactive power to the network.
Under no-load condition both the torque angle (λ) and the load angle (δ) are zero. The load angle is defined as the angle between the rotorís mmf (Ff) or flux (φf) and the resultant mmf (Fr) or flux (φr). The load angle (δ) is the most commonly used because it establishes the torque limits the machine can attain in a simple manner (discussed later). One must be aware that in many texts the name torque angle is used to indicate the load angle. The name torque angle is also sometimes given to indicate the angle between the terminal voltage (V1) and the excitation voltage (E1). This happens because the leakage reactance is generally very much smaller than the magnetizing reactance, and therefore the load angle (δ) and the angle between (V1) and (E1) are very similar. In this book the more common name power angle is used for the angle between (V1) and (E1). In Figure 1.24, the power angle is always shown as zero because the leakage impedance has been neglected in the ideal machine.
It is important at this stage to introduce the distinction between electrical and mechanical angles. In studying the performance of the synchronous machine, all the electromagnetic calculations are carried out based on electric quantities; that is, all angles are electrical angles. To convert the electrical angles used in the calculations to the physical mechanical angles, we observe the following relationship: