Karnaugh Maps

Introduction

So far we can see that applying Boolean algebra can be awkward in order to simplify expressions. Apart from being laborious (and requiring the remembering all the laws) the method can lead to solutions which, though they appear minimal, are not. The Karnaugh map provides a simple and straight-forward method of minimising boolean expressions. With the Karnaugh map Boolean expressions having up to four and even six variables can be simplified.

what is a Karnaugh map?

A Karnaugh map provides a pictorial method of grouping together expressions with common factors and therefore eliminating unwanted variables. The Karnaugh map can also be described as a special arrangement of a truth table. The diagram below illustrates the correspondence between the Karnaugh map and the truth table for the general case of a two variable problem. 

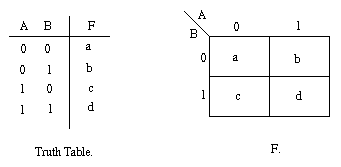
The values inside the squares are copied from the output column of the truth table, therefore there is one square in the map for every row in the truth table. Around the edge of the Karnaugh map are the values of the two input variable. A is along the top and B is down the left hand side. The diagram below explains this: 

The values around the edge of the map can be thought of as coordinates. So as an example, the square on the top right hand corner of the map in the above diagram has coordinates A=1 and B=0. This square corresponds to the row in the truth table where A=1 and B=0 and F=1. Note that the value in the F column represents a particular function to which the Karnaugh map corresponds.

Example 1:

Consider the following map. The function plotted is: Z = f(A,B) = A + AB 

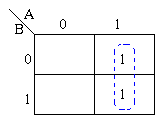
• Note that values of the input variables form the rows and columns. That is the logic values of the variables A and B (with one denoting true form and zero denoting false form) form the head of the rows and columns respectively.
• Bear in mind that the above map is a one dimensional type which can be used to simplify an expression in two variables.
• There is a two-dimensional map that can be used for up to four variables, and a three-dimensional map for up to six variables.

Using algebraic simplification,

Z = A + AB

Z = A( + B)

Z = A

Variable B becomes redundant due to Boolean Theorem T9a.

Referring to the map above, the two adjacent 1's are grouped together. Through inspection it can be seen that variable B has its true and false form within the group. This eliminates variable B leaving only variable A which only has its true form. The minimised answer therefore is Z = A.

Example 2:

Consider the expression Z = f(A,B) =  + A  + B plotted on the Karnaugh map: 

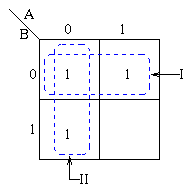
Pairs of 1's are grouped as shown above, and the simplified answer is obtained by using the following steps: 

Note that two groups can be formed for the example given above, bearing in mind that the largest rectangular clusters that can be made consist of two 1s. Notice that a 1 can belong to more than one group.  The first group labelled I, consists of two 1s which correspond to A = 0, B = 0 and A = 1, B = 0. Put in another way, all squares in this example that correspond to the area of the map where B = 0 contains 1s, independent of the value of A. So when B = 0 the output is 1. The expression of the output will contain the term  For group labelled II corresponds to the area of the map where A = 0. The group can therefore be defined as . This implies that when A = 0 the output is 1. The output is therefore 1 whenever B = 0 and A = 0 
Hence the simplified answer is Z =  +