Switching circuit theory

Switching circuit theory is the mathematical study of the properties of networks of idealized switches. Such networks may be strictly combinational logic, in which their output state is only a function of the present state of their inputs; or may also contain sequential elements, where the present state depends on the present state and past states; in that sense, sequential circuits are said to include "memory" of past states. An important class of sequential circuits are state machines. Switching circuit theory is applicable to the design of telephone systems, computers, and similar systems. Switching circuit theory provided the mathematical foundations and tools for digital system design in almost all areas of modern technology.

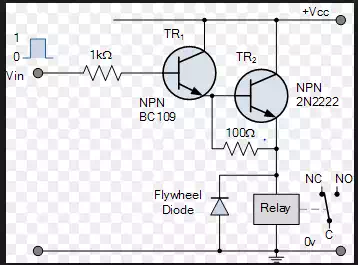
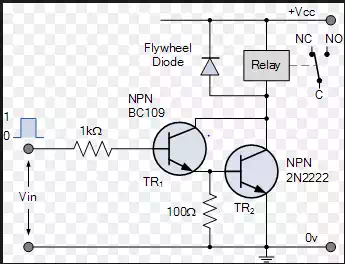
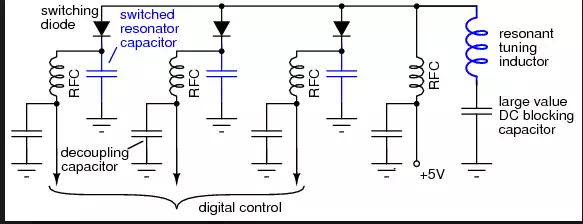
Switching circuts: