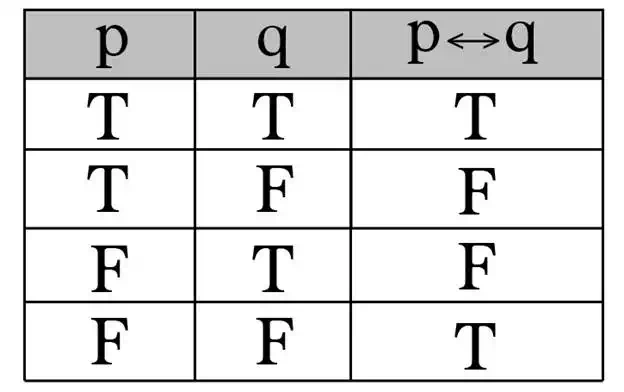
Truth Tables:

A truth table is a handy little logical device that shows up not only in mathematics, but also in Computer Science and Philosophy, making it an awesome interdisciplinary tool. The notation may vary depending on what discipline you’re working in, but the basic concepts are the same. This primer will equip you with the knowledge you need to understand symbolic logic. We’ll start with defining the common operators and in the next post I’ll show you how to dissect a more complicated logic statement.

Unary Operators

Unary operators are the simplest operations because they can be applied to a single True or False value.

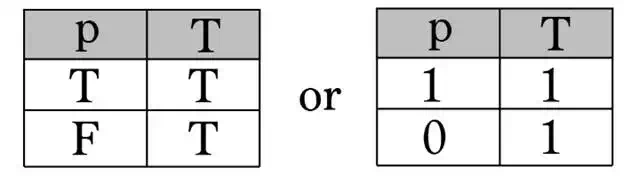
Identity

The identity is our trivial case. It states that True is True and False is False.

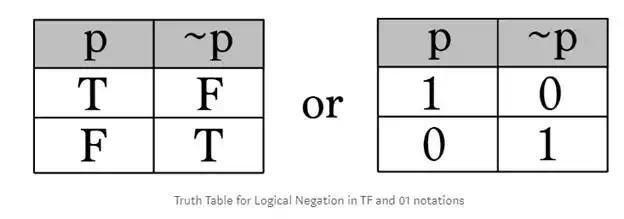
Negation

The negation operator is commonly represented by a tilde (~) or ¬ symbol. It negates, or switches, something’s truth value.We can show this relationship in a truth table. A truth table is a way of organizing information to list out all possible scenarios. We title the first column p for proposition. In the second column we apply the operator to p, in this case it’s ~p (read: not p). So as you can see if our premise begins as True and we negate it, we obtain False, and vice versa.

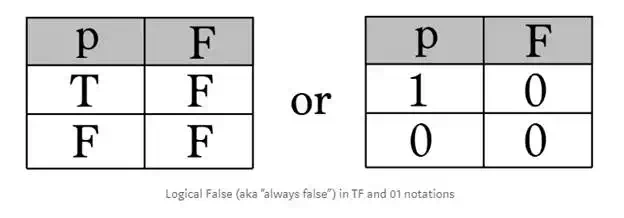
Logical True and Logical False

These are kinda strange operations. Logical true always results in True and logical false always results in False no matter the premise. These operations are often referred to as “always true” and “always false”.

Binary Operators

Binary operators require two propositions. We’ll use p and q as our sample propositions.

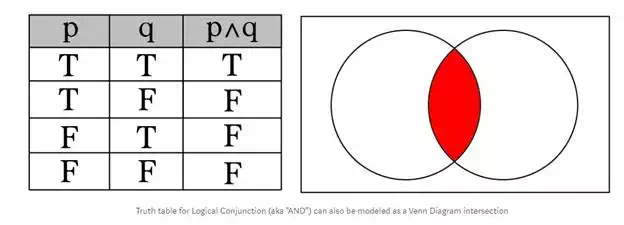
AND

The AND operator (symbolically: ∧) also known as logical conjunctionrequires both p and q to be True for the result to be True. All other cases result in False. This is logically the same as the intersection of two sets in a Venn Diagram.

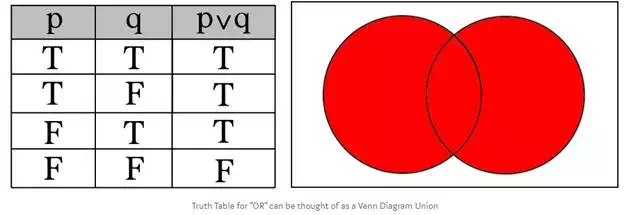
OR

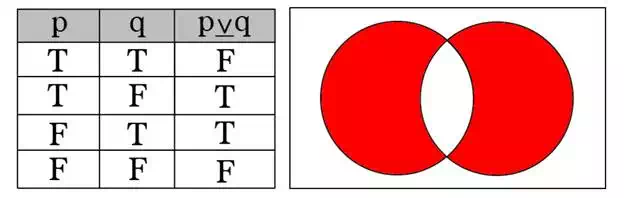
The OR operator (symbolically: ∨) requires only one premise to be True for the result to be True. This is equivalent to the union of two sets in a Venn Diagram

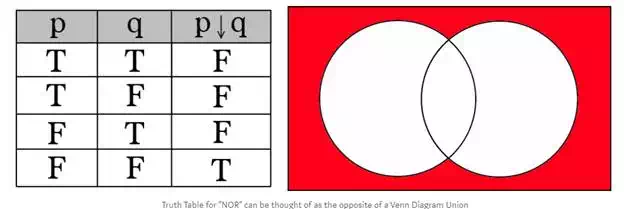
NOR

Logical NOR (symbolically: ↓) is the exact opposite of OR. It requires both p and q to be False to result in True.

XOR

Exclusive Or, or XOR for short, (symbolically: ⊻) requires exactly one True and one False value in order to result in True.

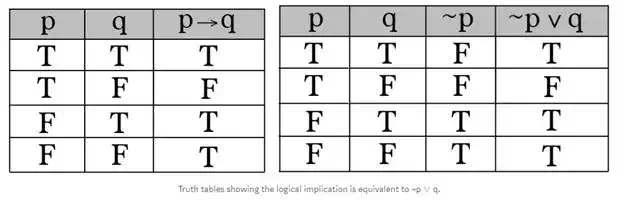
Implication

Logical implication (symbolically: p → q), also known as “if-then”, results True in all cases except the case T → F. Since this can be a little tricky to remember, it can be helpful to note that this is logically equivalent to ¬p ∨ q (read: not p or q)*. Let’s create a second truth table to demonstrate they’re equivalent. To do this, write the p and q columns as usual. Then add a “¬p” column with the opposite truth values of p. Lastly, compute ¬p ∨ q by OR-ing the second and third columns. Remember to result in True for the OR operator, all you need is one True value.