Use LTspice to Understand the LM741 OpAmp
The 741 op-amp shares with
most op-amps an internal structure consisting of three gain stages:
1. Differential amplifier — provides high
differential amplification (gain), with rejection of common-mode signal, low
noise, high input impedance, and drives a
2. Voltage amplifier — provides high
voltage gain, a single pole frequency rolloff,
and in turn drives the
3. Output amplifier — provides high current
gain (low output impedance), along with output current limiting, and output
short-circuit protection.
It's that
easy!
Well, not really.
Assuming you've
downloaded LTspice, open up the LM741 Model
in LTspiceIV\examples\Educational directory of
your LTspice
In part 1 we will mainly be
focusing on the input stage and the differential amplifier. Part 2 will consist
of the voltage amplifier and output amplifier.
Before reading further you
should be comfortable with the following equations that rule transistors:
IC=βIBIC=βIB
IE=(1+β)IBIE=(1+β)IB
What the Heck is a Differential Amplifier?
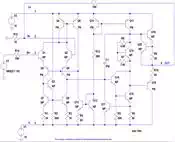
Figure 1 (Click to enlarge)
Current Mirrors
Well, before we get into a
differential amplifier we must understand the analog building
block called a current mirror. A current mirror is a circuit of the
configuration in Figure 1. Start with a current
IrefIref
which flows into the transistor Q1 in the figure below.
A transistor with its collector tied to its base is called a “diode connected
transistor” this creates an ideal diode. In turn, this produces a voltage drop
across the transistor Q1 of
VbeVbe
(about 0.7 volts). Now, since the base and emitter of Q2
is identical and the base-emitter voltage of the transistor Q2 equals the
transistor Q1, the same current that flows through Q1, flows through
Q2...Well...roughly the same. As you can see the
ImirrorImirror
is a factor of
ββ+2ββ+2
This works out to be roughly
98% of the current of Q1.
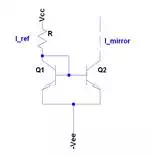
Figure 2
To derive the
equation for
ImirrorImirror
:
Iref=IB+ICIref=IB+IC
(Q1)
Iref=IB+βIB2Iref=IB+βIB2
Iref=IB(2+β)2Iref=IB(2+β)2
Therefore,
IB=2Iref2+βIB=2Iref2+β
Imirror=βIB2Imirror=βIB2
Imirror=2βIref2(2+β)Imirror=2βIref2(2+β)
Imirror=βIrefβ+2Imirror=βIrefβ+2
Differential Amplifiers
Let me confuse you first and
overstate the simplicity of its operation by saying that, simply put, a
differential amplifier is a type of amplifier that only amplifies the
difference between two voltages and nothing more (idealistically). Besides
using different variations of the word "amplify" and simplifying way
too many times in that last sentence, its operation is a little more complex
than I’ve led you to believe thus far. Let's get into the detail.
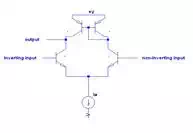
Figure 3 Long-Tailed Pair
This is a differential
amplifier, often referred to as a long-tailed pair. You can see this
fundamental analog building block
configuration being made between Q4, Q9, Q1, and Q2 of the schematic of the
LM741 above. The 741 has some additional components involved with its
differential pair input, but we will get into that later. Q4 and Q9 make the
current mirror of the PNP variety. Check your understanding by working out the
math much like we did for the NPN, taking note of the sign differentiation of a
PNP (I'll leave this as an exercise for you).
When the voltage at both
inputs is equal, then the current
IeIe
is split equally between the two transistors Q1 and Q2.
The purpose of
IeIe
is to allocate a set amount of current to the two
transistors such that when there is a difference at the inputs we get a
differential amplifier. That is, when we increase the voltage at the non-inverting
input relative to the inverting input Q2 gets more of the current than Q1, and
vice versa. I think this will be made clearer after a study of the simulation
below.
Differential Amplifier Simulation
Attach the two voltage
sources to your simulation as follows, take out the feedback and change both
input resistors to 1k as such:
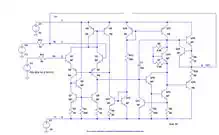
Figure 4
And Generate the
following output:
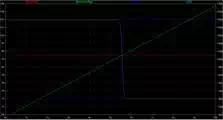
Figure 5
As the
non-inverting input reaches the inverting inputs voltage the current in Q1 and
Q2 is equal. Also note how the current in each differs depending on the difference in
voltage between the two inputs.
In the 741 the current
IeIe
of the long-tailed pair in figure 3 above is actually
produced by the additional circuitry in the input stage. The input stage is
made up of Q1, Q2, Q3, Q5, Q6, Q7, and Q8.
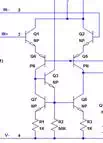
Q12, Q13
, and R13 are important to the input stage as well because they
create the reference current. The bias for the input stage is created with Q12,
Q13 and R4 and current mirror Q4, Q9.
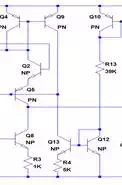
IrefIref
can be calculated as follows:
Iref=V+−VEBQ10−VBEQ12−(−V−)R13Iref=V+−VEBQ10−VBEQ12−(−V−)R13
where,
IrefIref
is the current flowing through the right side of the
circuit (Q10, R13, Q12)
Q12, Q13 and R4 create
a Widlar current source. The first step to
understanding a Widlar current source is to
do some research on the pioneer and analog legend Bob Widlar, an eccentric personality of the analog world, and inventor of the Widlar current mirror among many other things. He,
along with others I will mention, make up the original analog gods.
It’s VERY important to read about them.
Anyway, I digress... A Widlar Current source differs from a normal current
source because a resistor is added to the emitter of the output stage
transistor. In the 741's schematic this is resistor R4.This is more so a
practice in saving IC space when designing the chips. Instead of using large
resistors to create small currrents, the Widlar current source creates small currents with
small resistors. To calculate the current
ICIC
(of Q13) , which is the “output” of the Widlar current source follow the KVL around the base
emitter loop of this section of the circuit:
VBEQ12=VBEQ13+IEQ13R4=VBEQ13+(β+1)IBQ13R4VBEQ12=VBEQ13+IEQ13R4=VBEQ13+(β+1)IBQ13R4
Where,
IIN=ICQ12,IOUT=ICQ13IIN=ICQ12,IOUT=ICQ13
For a BJT,
VBE=VTln(ICIS)so,VBE=VTln(ICIS)so,
VTln(IINIS1)=VTln(IOUTIS2)+IOUTR4VTln(IINIS1)=VTln(IOUTIS2)+IOUTR4
IOUTR4=VTln(IINIOUT)IOUTR4=VTln(IINIOUT)
From here you can solve
iteratively.