Mesh Analysis and Dependent Sources

This article describes the technical aspects of Performing Mesh analysis with Dependent Sources.

Mesh analysis is a very handy tool to compute current within electronic circuits. From knowing the current within each mesh (section), we can solve for voltage and power (watts) at each component. Engineers and designers use this information to select correct parts that won’t emit the magic white smoke when power is applied.

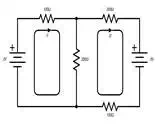
We can divide the example above into two meshes, I1 and I2. I1 designates a virtual current in mesh 1. I2shows virtual current in mesh 2. Mesh current flow is usually depicted in a clockwise direction. From here, we write each mesh as a linear equation and use a solving tool to find I1 and I2.

Using Kirchhoff’s Voltage Law (KVL), mesh I1 would be written as:

−3 v+100Ω(I1)+200Ω(I1−I2)=0−3 v+100Ω(I1)+200Ω(I1−I2)=0

The I1-I2 is because the current flowing thru the center 200Ω resistor is the difference between the two meshes. Due to the clockwise flow of I1, the (-) side of the battery is recorded as the voltage.

This formula can be rewritten as:

I1(300Ω)−I2(200Ω)=3 vI1(300Ω)−I2(200Ω)=3 v

Mesh I2 can be described in electrical terms as:

6 v+100Ω(I2)+200Ω(I2−I1)+200Ω(I2)=06 v+100Ω(I2)+200Ω(I2−I1)+200Ω(I2)=0

Simplified and rewritten, this comes out to:

−I1(200Ω)+I2(500Ω)=−6 v−I1(200Ω)+I2(500Ω)=−6 v

Here is an online linear equation solver (which will make the solving much simpler). To minimize the chance of symbols being misunderstood, it is best to rename I1 to “a” and I2 to “b”.

The finished query is:

300a−200b=3300a−200b=3

,   [Equation 1]

and,

−200a+500b=−6−200a+500b=−6

   [Equation 2]

The answers are:

I1(“a”)=31100 A−−−−−−I1(“a”)=31100 A_

or

2.727 mA2.727 mA

,

and,

I2(“b”)=−3275 A−−−−−−−I2(“b”)=−3275 A_

or

−10.909 mA−10.909 mA

Remember that the current in the center 200-Ω resistor is (I1 – I2). So,

2.727 mA–(−10.909 mA)=13.636 mA−−−−−−−−−2.727 mA–(−10.909 mA)=13.636 mA_

The batteries would be considered as an independent voltage source. What would happen if we replaced one of them with a voltage controlled voltage source (VCVS), such as a vacuum tube or FET circuit?

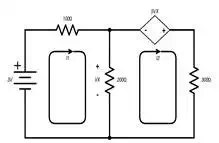
The formula for the I1 mesh would be identical to the previous example.

It is:

I1(300Ω)−I2(200Ω)=3 vI1(300Ω)−I2(200Ω)=3 v

or for the solver:

300a−200b=3300a−200b=3

   [Equation 3]

Mesh I2 contains the VCVS dependent voltage source. The gain is noted by the 5VX and the source of the control voltage is seen as the nodes on each side of the center resistor. The formula for I2 is no more complicated than it is for I1.

Starting at the 200-Ω resistor and using KVL we have:

200Ω(I2−I1)–5VX+300Ω(I2)=0200Ω(I2−I1)–5VX+300Ω(I2)=0

.

In a more usable and condensed form, the equation is:

−I1(200Ω)+I2(500Ω)=5VX−I1(200Ω)+I2(500Ω)=5VX

   [Equation4]

The dependent voltage source is a ratio and not a fixed number at this point. To be able to solve this system, we need to write the formula for VX. This is found multiplying the resistance 200 Ω by the current.

Since this resistor is used by both meshes, the current is:

I1−I2I1−I2

VX is:

200Ω(I1−I2)200Ω(I1−I2)

   [Equation 5]

VX will be annotated as “c” for the solver.

Putting the three linear equations (Equations 3, 4 and 5) into a Wolfram Alpha friendly syntax, we have:

300a−200b=3300a−200b=3

,

−200a+500b=5c−200a+500b=5c

,

c=200(a−b)c=200(a−b)

The results of the equation are: I1 has a current of 21.429 mA, I2 has a current of 17.143 mA, and VX has a voltage of 0.857 Volts. Our dependent source has a gain of 5 and therefore is producing 4.286 Volts. At this point someone is thinking “Hey, wait a minute. Why does I1 have more current in the second example if the dependent source’s voltage is lower than the battery it replaced?” Nice catch! We swapped the polarity for the dependent source and both I1 and I2 currents jumped. Hopefully this was planned and our circuit isn’t smoking like a sock in the toaster.

Other dependent sources include Current Controlled Voltage Sources (CCVS), Voltage Controlled Current Sources (VCCS), and Current Controlled Current Sources (CCCS). A bipolar junction transistor is a good example of a CCCS.

The comprehension of mesh analysis with dependent sources is important when planning circuits that utilize amplifiers or amplifying components. The methods are nearly the same as without dependent sources except that more information needs to be presented to achieve a solution.