Sensor fusion is the art of combining multiple physical sensors to produce accurate "ground truth", even though each sensor might be unreliable on its own. Learn about the how and why behind sensor fusion.
How do you know where you are? What is real? That’s the core question sensor fusion is supposed to answer. Not in a philosophical way, but the literal “Am I about to autonomously crash into the White House? Because I’ve been told not to do that” way that is built into the firmware of commercial Quadcopters.
Sensors are far from perfect devices. Each has conditions that will send them crazy.
Inertial Measurement Units are a classic case—there are IMU chips that seem superior on paper, but have gained a reputation for “locking up” in the field when subjected to certain conditions, like flying 60kph through the air on a quadcopter without rubber cushions.

An IMU chip. Image courtesy of the University of Michigan.
In these cases the IMU can be subject to vibrations—while inside spec—that can match harmonics with micromechanical parts. The IMU may have been designed for use in a mobile phone with a wobbler, not next to multiple motors humming at 20,000 RPM. Suddenly the robot thinks it’s flipping upside down (when it’s not) and rotates to compensate. Some pilots fly with data-loggers, and have captured the moment when the IMU bursts with noise immediately before a spectacular crash.
So, how do we cope with imperfect sensors? We can add more, but aren't we just compounding the problem?
Your blind spots get smaller the more sensors you have. But the math gets harder in order to deal with the resulting fuzziness. Modern algorithms for doing sensor fusion are “Belief Propagation” systems—the Kalman filter being the classic example.

Naze32 flight controller with onboard "sensor fusion" Inertial Measurement Unit. This one has flown many times.
At its heart, the algorithm has a set of “belief” factors for each sensor. Each loop, data coming from the sensors is used to statistically improve the location guess, but the quality of the sensors is judged as well.
Robotic systems also include constraints that encode the real-world knowledge that physical objects move smoothly and continuously through space (often on wheels), rather than teleporting around like GPS coordinate samples might imply.
That means if one sensor which has always given excellent, consistent values starts telling you unlikely and frankly impossible things (such as GPS/radio systems when you go into a tunnel), that sensors' believability rating gets downgraded within a few millisecond iterations until it starts talking sense again.
This is better than just averaging or voting because the Kalman filter can cope with the majority of its sensors going temporarily crazy, so long as one keeps making good sense. It becomes the lifeline that gets the robot through the dark times.
The Kalman filter is an application of the more general concepts of Markov Chains and Bayesian Inference, which are mathematical systems that iteratively refine their guesses using evidence. These are tools designed to help science itself test ideas (and are the basis of what we call “statistical significance”).
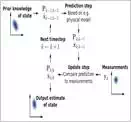
Representation of a Kalman filter. Image created by Petteri Aimonen via Wikimedia Commons.
It could, therefore, be poetically said that some sensor fusion systems are expressing the very essence of science, a thousand times per second.
Kalman filters have been used for orbital station-keeping on space satellites for decades, and they are becoming popular in robotics because modern microcontrollers are capable enough to run the algorithm in real time.
Simpler robotic systems feature PID filters. These can be thought of as primitive Kalman filters fed by one sensor, with all the iterative tuning hacked off and replaced with three fixed values.
Even when PID values are autotuned or set manually, the entire “tuning” process (adjust, fly, judge, repeat) is an externalized version of Kalman with a human doing the belief-propagation step. The basic principles are still there.
Real systems are often hybrids, somewhere between the two.
The full Kalman includes “control command” terms that make sense for robots, as in: “I know I turned the steering wheel left. The compass says I’m going left, the GPS thinks I’m still going straight. Who do I believe?”
Even for a thermostat—the classic simplest control-loop—a Kalman filter understands that it can judge the quality of thermometers and heaters by fiddling with the knob and waiting to see what happens.
Individual sensors usually can’t affect the real world, so those terms drop out of the math and much power goes with them. But you can still apply the cross-checking belief propagation ideas and “no teleporting” constraints, even if we can’t fully close the control loop,
For the rest of the article we’ll be concerned with physical position, but the same ideas apply to any quantity you care to measure. You might think that multiple backup sensors of the same type are the way to go, but that often combines their identical weaknesses in unfortunate ways. Mixed systems are stronger.
Let’s state the general problem as “I don’t want my quadcopter to crash”, defining the failure condition as any intersection of the fast-flying robot with the fractal surface known as “the unforgiving ground”.
We'll quickly discover there's no single commodity sensor we can absolutely trust 100% of the time. So why aren't robots raining out of the sky? Because each solves a different fragment of the bigger Sudoku puzzle, until only the truth remains.
Let's go over some typical sensors you might find on a quadcopter and discuss their strengths, weaknesses, and overall place in this "Sudoku puzzle" of sensor fusion.
This is the obvious go-to, but oh the limitations! There's a sample error of maybe two meters, and the deviation will drift with the satellites.
If you want to use a GPS to get a position accurate to the centimeter, you need to nail it in place and take measurements over the course of days. That’s not what we want. Moving through the air at speed, even a 100Hz GPS unit can’t do temporal smoothing. That’s 20 times slower than the flight controller's main event loop.
GPS also cannot tell you which way you are facing. Only which way you are moving.
Also, Z-resolution (height) can be 1/10th as reliable as latitude and longitude. We have to give the ground perhaps 20 meters leeway.
Oh, and GPS alone doesn’t tell you how far above ground you are, only how far above sea-level. The logical fix is to take a reading before takeoff—but then we have another 20-meter error bar in the mix. And there are ground-plane effects on GPS signals which are different in flight, so we can’t assume the errors will cancel over the long term - although they will at first!
And it still doesn’t stop us from flying into hills.

A commodity GPS receiver that can be interfaced easily with microcontrollers over I2C.
One GPS is not enough. We can’t reliably fly within 20-40 meters of flat ground, which is at least five stories in the air, and that’s a long way up for a safety margin. Don’t get me wrong, being able to locate yourself anywhere in the world with a 20-meter vertical error margin is utterly amazing… but it won’t stop us from crashing. Not without a differential GPS ground station in the loop, expensive high-speed receivers, and some damn good topological maps.
Sonar, Lidar, Radar / Optical Flow
So if triangulating yourself using satellites isn’t the best way to avoid the ground, let's just try to “see” it directly!
There are at least three off-the-shelf ranging technologies that emit a ping and see how long it takes to bounce back: SONAR, LIDAR, and apparently RADAR modules are now available.
However, these sensors have weaknesses:
● Absorption
Some surfaces just don’t bounce the signal. Curtains and carpet absorb ultrasound, dark paints absorb lidar, and water absorbs microwaves. You can’t avoid what you can’t see.
● Cross-talk
Less obvious is what happens when you put multiple identical sensors near each other. How do you know the ‘ping’ you detected is yours? Even single sensors must cope with cross-talk from themselves, waiting long enough for echoes to fade away.
It’s possible to ‘code’ the signals (basically, encrypt them) so each ping is unique, but that raises the complexity of the device. The second best solution is to semi-randomize your ping schedule, so you don’t lock timing and get consistently tricked by a synchronized ping.
Optical flow sensors are a different approach, using a camera to see if everything in shot is getting bigger (indicating the ground/wall is coming up fast) or smaller (when the obstruction is going away) or sliding sideways. Cameras don’t interfere with each other like sonar, and if you're really clever you can estimate tilt and other 3D properties.
Optical flow sensors still suffer from the ‘absorption’ weakness. You need a nice textured surface for them to see the flow, just as the optical mice they’re based on don’t work on glass. They are becoming popular as the flow calculations are now something you can fit into an FPGA or fast embedded computer.

Image sensors (such as this 2K resolution Raspberry Pi camera) can be used for "optical flow" obstacle avoidance.
● Geometry
The last issue is geometric. Consider the physical sensor flying on a quad. If you are at an angle then Pythagoras says the ground will seem to be further away than it really is. Tilt enough and we won't see it at all, though we are centimeters from crashing.
To correct for that, we need to know about our inclination. And that means...
Gyros get lumped in with the accelerometer and referred to as an ‘IMU’, but the reason they appear so often together is they naturally cover each other’s major weakness. They are the classic fusion pair.
But, individually, the gyro is the best and cleanest single source of sensor data you’re going to get for continuous position measurement.
Without going into too much detail, gyros are built from micromechanical tuning forks that are etched into the surface of the chip. When the chip is rotated, there are forces on some of the tuning forks, and they change pitch against each other. (Alas, there are no tiny spinning tops— that would be too simple.)
MEMS gyros are almost immune to every motion except rotation. Even severe vibration doesn’t affect them (within spec) because that's lateral acceleration.
If you look into the internal control loop of a multirotor, it is the gyro which the flight controller is using to stay level in the air. Some rate-mode pilots turn the accelerometer off entirely to give the gyro more bandwidth. That’s a clue to how important the gyro is.
Interior of a MEMS gyroscope sensor. Image courtesy of Geek Mom Projects.
If you knew where you were a half-millisecond ago and you want to know what’s changed since, gyros are fast, accurate, and reliable. They don’t need bouncy surfaces or satellites. Quads literally could not fly upright without them.
The weakness of gyros is drift. They seem to slowly rotate around a random axis, no matter how hard you try. It takes a couple of minutes per rotation, but even an immovable brick will appear to gently spin. Accumulating relative samples to get an ‘absolute’ estimate also adds together the error bars. The rising gyro error needs to be ‘zeroed’ regularly by an outside absolute reference mark.
This is why accelerometers are a gyro's best friend: because it detects an absolute ‘down’ reference (at least, while they’re in Earth’s gravity).
Well, on average anyway. From moment to moment, it’s picking up gravity, linear acceleration, centrifugal forces from rotation, vibration, loud noises, and of course sensor imperfections.
Accelerometer data is therefore some of the noisiest and least trustworthy of all, despite the high sample rate and good MEMS sensor accuracy which is usually as good as the gyro. It’s picking up multiple ‘signals’ that have to be disambiguated. But it is the sensitivity to all these different signals that makes it so versatile. It hears everything.
Acceleration is also two integration steps away from the thing we really want to know—position—so we have to sum up lots of deltas and error bars to go from measured acceleration to estimated speed, and then we have to do it again to get to estimated position. The errors pile up.
And that is why GPS is the accelerometer's best friend: because it regularly ‘zeroes’ out the growing position error, the same way the accelerometer gently zeros out the orientation error of the gyro.

Example of an accelerometer sensor chip. Image courtesy of Parallax.
The good ol' compass shouldn’t be neglected. Like the accelerometer, however, it is generally used as a way of reigning in the long-term gyro drift. Knowing which way is up is more useful than knowing which way is magnetic north— but, with both, we can know our true absolute orientation on Earth.
Magnetometer samples are also very noisy, especially if you’ve got motors nearby. They’re subject to all kinds of environmental effects, whether steel building frames or funny rocks.
They're often paired up with GPS receivers because, again, they counter each other’s greatest weakness while being otherwise closely matched. One gives rough absolute position while the other gives rough absolute direction. If your robot is confined to the ground on wheels (instead of flying around like a fool) that's really all you need.
Twice as Powerful. Twice as Deadly!
“Sensor fusion” is now clearly just the process of taking all these inputs and hooking them up to something like a Kalman filter. Notice the thing we want to know, “distance above the ground”, is not something that any of our sensors directly measure. (Even the sonar/radar pings measure distance to some ground.) The truth about the ground is inferred.
The logical stage beyond Kalman filters is Hidden Markov Models (HMMs), which we have invoked by saying there was a “hidden” property called vertical height that we don't directly observe (though there are many measurements we take that indirectly suggest what it is). After gathering enough evidence, we can be pretty certain of the true answer, despite the noisy sample data.
Or, at least, certain enough not to crash.
It sounds like you’d want to pull all your sensor data into your primary microcontroller and do the math there, but be very careful of temporal aliasing effects. If the timing of one sensor drifts with respect to the others, then fusion results can get jittery in odd ways.
Think of what happens if you have a sensor block that you slide across a table, but half-way across you flip it 90 degrees onto its side.
The IMU should see that as “sliding sideways, rotate 90, sliding upwards”— integrating that into a real position in space you should get a flat, straight line. But if the “flip 90” gyro signals are delayed (or just timestamped badly) then the accelerometer vectors won't get properly rotated back into the plane of the table for each instant of time, and there will be some vertical drift as motion 'leaks' into the wrong axis. Not due to any inaccuracies in the sensors, but purely because of the processing sequence.
This is why some IMUs do it all themselves. The popular MPU-6050 has its own firmware, a gyro, and accelerometer onboard and can also have an external magnetometer attached. After fusion, the IMU reports back an idealized motion vector to the microcontroller that gives more consistent results. Of course, there's always a tradeoff: The fused motion updates (for this chip, at least) come at a lower rate than raw values.
If you have a sophisticated control filter, raw sensor values are a more ‘honest’ input for algorithms that thrive on that information. But if you’re fine with slow but precise (or you only care about the final answer) let the chip do the fusing for you.