Understanding the Delta-Sigma ADC

Learn more about the Delta-Sigma ADC (analog-to-digital converter) which relies upon oversampling and noise shaping to achieve high-resolution conversions.

ADCs can be described as either Nyquist-rate or oversampled converters. In my previous article, Deciphering Resolution and Sampling Rate, I explained how sampling in the Nyquist-rate family of converters works and one of the key concepts this type of converter relies upon, the Nyquist Criterion.

The Delta-Sigma ADC works a little differently from the Nyquist-rate ADC. It relies upon oversampling and noise shaping to achieve high-resolution conversions.

My previous article, Understanding the Successive Approximation Register ADC, demonstrates a weakness of this Nyquist-rate architecture: Its accuracy and linearity, and thus its maximum effective resolution, are limited by the imperfections of analog components such as the DAC.

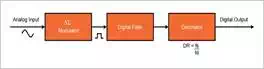
The oversampled family of converters, to which the Delta-Sigma ADC belongs, aims to overcome the limitations of Nyquist-rate converters. The Delta-Sigma ADC consists of a modulator, a filter, and a decimator as shown below. Delta-Sigma ADCs are approximately 75% digital.

By introducing more complex digital circuitry and oversampling the data, they attempt to reduce the requirements for accurate analog components that can be considered the limiting factor in other ADC architectures.

Oversampling

In order to understand the concept of oversampling, an analysis in the frequency domain is required.

If we consider the example of a sine wave at the input to the data converter, according to the Nyquist Criterion, the minimum sampling frequency is defined as twice the bandwidth of the signal.

$Title: \epsilon= \frac{\pm{q}}{2}=\pm{A}\cdot 2^{-N}$

For our example of a sine wave, we see a peak at the frequency of interest but lots of noise, as well, as shown below:

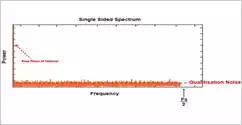
This noise is known as quantization noise (PDF) and is due to the fact that the samples of the continuous input sine wave can only take a finite number of discrete states determined by the resolution of the ADC. This random quantization error exists within the Nyquist band extending up to Fs/2 and can be described as:

$Title: \epsilon= \frac{\pm{q}}{2}=\pm{A}\cdot 2^{-N}$

From this, we can determine the signal to quantization noise ratio as:

$Title: 10\text{log}_{10}\frac{P_s}{P_\epsilon}=1.76+6.02N (dB)$

Thus, in a Nyquist-rate ADC, we improve the SQNR (signal-to-quantization-noise ratio) by increasing the resolution (denoted by N) of the ADC. For a more in-depth explanation of these formulas, please refer to my previous article, Deciphering Resolution and Sampling Rate.

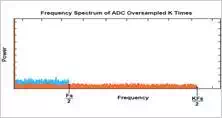
If instead we now increase the oversampling frequency from Fs to KFs, as shown below, the quantization noise in the region Fs/2 is reduced. The SQNR is actually the same.

The quantization noise, however, is spread over the larger frequency range. By incorporating a filter into Delta-Sigma ADCs, some of this quantization noise can be removed. Thus, this reduction in quantization noise over the frequency range of interest enables the low-resolution Delta-Sigma architecture to perform high-resolution analog-to-digital conversions.

The SQNR improves by 6 dB if we increase the sampling rate by a factor of 4. In other words, each time we quadruple the sampling rate, we gain the equivalent of adding 1 bit to the resolution of the ADC. With oversampling alone, in order to achieve a 12-bit resolution, the input must be oversampled by a factor of 411. Or, more generally, for an N-bit increase in resolution, we must oversample by a factor 22N.

Fortunately, another technique is used known as noise shaping to enable a gain of more than 6 dB.

Noise Shaping

The block diagram of a first order Delta-Sigma Modulator is shown below. This consists of a difference amplifier, an integrator, a comparator, and a switch. The switch, or 1-bit DAC, switches a negative or positive reference voltage into the negative input of the amplifier.

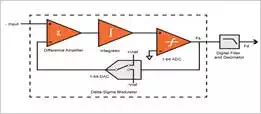
In this architecture, if the input signal has increased, the 1-bit ADC, which is simply a comparator, generates a one. If it has decreased, it generates a zero. As such, the Delta-Sigma modulator transmits the changes in, or the gradient of, an input signal.

As with oversampling, noise shaping is best explained in the frequency domain. A frequency domain model of the modulator is shown below:

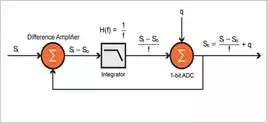
The integrator in this architecture acts as a lowpass filter to the input signal. Quantization noise is added to the signal output of this filter due to the 1-bit conversion process. The output of the modulator can be represented using the equation below.

$Title: S_o=\frac{S_i+qf}{f+1}=\frac{S_i}{f+1} +\frac{qf}{f+1}$

The first term in this equation can be considered the signal term and the second term can be considered the noise term. As the frequency approaches zero, it can be seen that the noise term approaches zero and the output of modulator approaches Si. As the frequency is increased, the noise term approaches q and the signal term approaches zero. As such, the integrator acts as a highpass filter for the quantization noise.

Higher order Delta-Sigma ADCs, with more than one stage of integration and summation in the modulator, can be used to achieve further noise shaping.

Digital Filtering and Decimation

The Delta-Sigma modulator pushes the noise to higher frequencies to increase the resolution of the ADC and performs the conversion of the analog input to a bit stream. The digital filtering and decimation stage are used to filter out the high-frequency noise and reduce the data rate to a usable amount.

The filter used is most often a type of averaging filter known as a sinc filter. Because the noise has been pushed to high frequencies, the lowpass filter response acts to attenuate the quantization noise. Thus, a high-resolution version of the original signal has been obtained.

The output data rate of the filter is the same as the sampling rate (Fs). The filter has reduced the frequency bandwidth of the signal. As such, and according to the Nyquist Criterion, most of the samples do not contain any useful information.

Decimation is the process of discarding the unnecessary samples and is used as a mechanism to reduce the data rate to a usable value whilst maintaining the information according to the Nyquist Criterion.

The Delta-Sigma ADC has two sampling rates, the input sampling rate (Fs) and the output data rate (Fd). The ratio of Fs to Fd is known as the Decimation Ratio (DR). By reducing the filter’s passband and increasing the DR, whilst maintaining the same Fs, the effective number of bits (ENOB) for a Delta-Sigma ADC can be increased. Likewise, the bandwidth of the ADC can be increased at the expense of ENOB.

Summary

Strengths of the Delta-Sigma ADC

● Resolution less reliant on analog components

● Extremely high resolution achievable

Weaknesses of the Delta-Sigma ADC

● Low sampling rates for high resolutions

Applications of the Delta-Sigma ADC

Delta-Sigma ADCs offer very high resolution with an ENOB of 20-24 bits. This makes them a good choice for precision industrial measurement applications, thermocouple temperature measurement, and voiceband applications.