From Filter Specs to
Window Parameters in FIR Filter Design
Learn how to
use filter specs to help choose the best window parameters for your FIR filter
design.
The previous article in this series discussed that a tapered window, such as
a Bartlett, can give better PSL than a rectangular window which has abrupt
variation in the time domain.
In this article, first, we
will review other popular windows. Then, we will clarify the design procedure
by calculating the cutoff of the ideal
filter, window type, and window length from given filter specs, namely,
ωpωp
,
ωsωs
and
δδ
.
In other words, a specific
application gives us
ωpωp
,
ωsωs
, and
δδ
, and now we need to find the required ideal filter response, window type,
and window length to design an FIR filter. The relation between these
parameters is the subject of this article.
Other Popular Window Functions
Fortunately, the Bartlett and
the rectangular windows are not the only options in FIR filter design and many
other windows have been developed.
Table I shows some of the
most popular windows along with their important properties. In Table I,
Bartlett, Hann, and Hamming have equal approximate main lobe
width, but we can observe the general trade-off between the PSL and the main
lobe width. The rectangular window has the smallest main lobe width and the
largest PSL, whereas the Blackman has the widest main lobe and the smallest PSL.
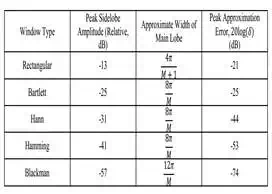
Table I Popular windows and their
properties.
The Fourier transform of
three windows, Bartlett, Hann, and Hamming with
M=21M=21
, are plotted in Figure (1). The mentioned trade-off is observed in these
three windows, too. As the PSL reduces, the main lobe width increases.

Figure (1) Bartlett, Hann, and Hamming of length
M=21M=21.
In addition to PSL and
approximate main lobe width, Table I gives, for each window, the peak
approximation error, which is the deviation from the ideal response (denoted by
δδ
) expressed in dB. This is an
important parameter which allows us to choose an appropriate window based on
the requirements of an application. Peak approximation error determines how
much deviation from the ideal response we expect for each of the window types.
This is illustrated in Figure (2).
As will be discussed in the
following section, the deviations from the ideal response in the pass-band and
stop-band are approximately equal when using the window method to design FIR
filters, i.e.,
δ1=δ2=δδ1=δ2=δ
. Therefore, we can select the suitable window based on how much ripple is
allowed in the pass-band or how much attenuation is needed in the stop-band.
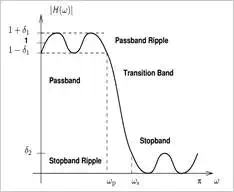
Figure (2) Deviations from the ideal response in the pass-band,
δ1δ1
, and in the stop-band,
δ2δ2
. Image courtesy ofthe University of
Michigan (PDF).
Important Properties of the Window Method
In this section, some of the
most important properties of the window method, which are necessary for design
procedure, will be discussed. We need to find the cutoff of
the ideal filter, window type, and length based on given filter specs, namely,
ωpωp
,
ωsωs
, and
δδ
. In other words, a specific application gives us
ωpωp
,
ωsωs
, and
δδ
, and now we need to find the required ideal filter response,
window type, and window length to design an FIR filter. The relation between
these parameters is the subject of this section.
Please note that we
are not trying to give strict and thorough proofs. Instead, our goal is to
provide some insight into these properties so that you do not need to memorize
them.
1- Ideal Cutoff Frequency,
ωpωp
and
ωsωs
When using the window method
to design an FIR filter, we start from filter specs
ωpωp
and
ωsωs
. Having
ωpωp
and
ωsωs
, we should find a suitable ideal filter with cutoff frequency
ωcωc
, then find the FIR filter related to this ideal filter.
The question is: What is the
relation between
ωpωp
,
ωsωs
and
ωcωc
?
To answer this question,
consider Figure (3). This figure shows the slide-and-integrate process,
discussed ina previous article of this series, to calculate the convolution of the
window and the ideal filter. The ideal desired frequency response, the designed
filter, and the shifted window spectrum are shown in this figure. Note that the
Fourier transform of the window is approximated with only the main lobe and the
first sidelobes (the amplitude of the
other sidelobes is assumed to be zero). The
window is shifted so that its peak is exactly on the abrupt cutoff of the ideal filter.
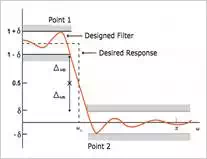
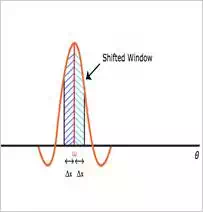
Figure (3) The Fourier transform of the window is symmetric around its
peak and hence
ωc=ωp+ωs2ωc=ωp+ωs2
First,
assume that we shift the window from its current position by
ΔxΔx
to the right. The part of the window
marked by the red dashed lines will go out of the passband of the ideal filter.
Hence, the convolution value will decrease by, letís say
Δ1Δ1
.
Now, assume that we shift the
window from its position in Figure (3) by
ΔxΔx
to the left. The part of the window
which is marked by the blue dashed lines will go inside the passband of the
ideal response. How much will the convolution increase by?
Since the Fourier transform
of the window is symmetrical around its peak, the convolution will increase by
Δ1Δ1
. Note that this reasoning may be invalid if we do not assume that the
main lobe with is much smaller than the passband of the ideal filter (Why do
you think this might be the case? See if you can come up with the answer on
your own.)
With this symmetrical behavior in mind, consider
ωpωp
where the magnitude of frequency
response is
1−δ1−δ
and where
ΔωpΔωp
, as shown in Figure (3), will be
1−δ−0.51−δ−0.5
in this case.
At
ωsωs
, the magnitude of frequency response will be
δδ
and
ΔωsΔωs
, as shown in Figure (3), will be
0.5−δ0.5−δ
. Since
Δωp=ΔωsΔωp=Δωs
, we can conclude that frequency shifts corresponding to these two cases
are equal.
In other words,
ωc=ωp+ωs2ωc=ωp+ωs2
. Notice that, as shown in the figure, the magnitude of the designed
filter is approximately 0.5 at
ω=ωcω=ωc
. This is quite obvious in the special case of ignoring all the sidelobes and keeping only the main lobe.
2- Peak Approximation Error in Pass-Band
and Stop-Band
The peak approximation error
in the pass-band is equal to the peak approximation error in the stop-band. To
get a feeling for this, consider Figure (4) which is taken from a previous article in this series.
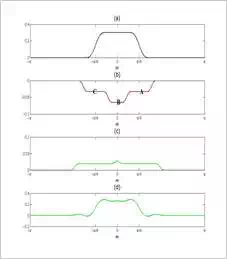
Figure (4) Convolution of
Hd(ω)Hd(ω)
with (4a)
T1T1
(4b)
T2T2
(4c)
T3T3
and (4d)
T1+T2+T3T1+T2+T3
This figure shows the
convolution of the ideal response with triangular approximations of the main
lobe,
T1T1
, the first sidelobe,
T2T2
, and second sidelobe,
T3T3
.
Peak approximation error is
directly related to the PSL of the window. In fact, other side lobes are much
smaller than the first sidelobe and have a
negligible effect on the peak approximation error.
If we assume that the main
lobe width of the window is much smaller than the cutoff frequency,
ωcωc
, of the ideal filter,
Hd(ω)Hd(ω)
, the convolution of
Hd(ω)Hd(ω)
with
T1T1
and
T2T2
will be similar to Figure (4a) and
(4b), respectively.
We know that the convolution
of
Hd(ω)Hd(ω)
with
T2T2
determines the ripples in the
frequency response of the designed filter. In Figure (4b),
Hd(ω)∗T2Hd(ω)∗T2
has a variation of
one step, A and C, at the stop-band. Besides,
Hd(ω)∗T2Hd(ω)∗T2
has a variation of
only one step, B, in the pass-band.
Since the variation of
Hd(ω)∗T2Hd(ω)∗T2
is the same in both the pass-band and
the stop-band, we expect the peak approximation error to be the same in both
the stop-band and pass-band.
3- Transition Band and the Main Lobe Width
Having
ωpωp
and
ωcωc
, we need to determine the main lobe width of the required window. To this
end, we examine Figure (3) one more time. As shown in Figure (3), we only
consider the first sidelobe.
In this figure, if we shift
the window to the left so that the main lobe is completely inside the passband
of the ideal filter response, we will get the maximum of the convolution,
point1 in the figure.
On the other hand, if we
shift the window to the right so that the main lobe is right out of the ideal
response, point2 will be achieved.
Therefore, the distance
between point1 and point2 is almost equal to the main lobe width. As a result,
the transition band,
ωs−ωpωs−ωp
, will be smaller than the main lobe width. However, we can use the
transition band as an estimate of the required main lobe width.