The Bartlett Versus the Rectangular Window

In this article, we will discuss the fact that choice of different window functions involves a trade-off between the main lobe width and the peak sidelobe (PSL).

Background

To gain more insight, we will calculate the Fourier transform of a triangular window using the Fourier transform of a rectangular window. The connection between these two windows helps us to better understand the trade-off involved when you choose between different window functions.

In the first article of this series, we saw that truncation of the impulse response of an ideal filter is equivalent to multiplying the impulse response by a rectangular window. The Fourier transform of the truncated impulse response will exhibit ripples in the pass-band and stop-band. Moreover, the transition band of the achieved filter will be considerably wider than the ideal response.

The second article showed that the main lobe width of a rectangular window determines the width of the filter transition band, whereas the PSL of the window affects the ripples in the pass-band of the filter. It was shown that as we reduce the main lobe width and the PSL, the achieved filter gets closer to the ideal response.

One way to reduce the main lobe width is to increase the number of samples,

MM

. However, the PSL of a rectangular window is almost independent of

MM

. Is there any other way to reduce the main lobe width and simultaneously get a smaller PSL? Or a better question: Is there another window which can give better performance in terms of main lobe width and PSL? Or at least is there a window which can give a smaller PSL? Because if we can find a window which has, at least, a smaller PSL, we can probably reduce the main lobe width of this specific window by choosing a large

MM

.

Based on the previous discussion, we will ignore the main lobe width and focus on achieving a smaller PSL than that of a rectangular window.

Consider the normalized Fourier transform of a rectangular window as shown in Figure (1) of the previous article, shown here:

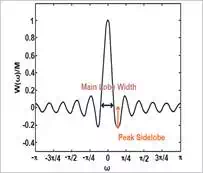
Figure (1)

W(ω)MW(ω)M

for

M=21M=21

If we square this spectrum, the peak of the sidelobe, which is less than 1, will decrease compared to the main lobe. Therefore, an unknown window,

wx[n]wx[n]

, whose Fourier transform is equal to the squared of the rectangular window will have a smaller PSL. Multiplying in the frequency domain corresponds to convolution in the time domain. As a result,

wx[n]wx[n]

must be the convolution of two rectangular windows of the same length, which is a triangular window.

To examine this idea, in the following section, we will calculate the Fourier transform of a triangular (Bartlett) window and we will highlight its connection with the Fourier transform of a rectangular window to gain more insight to the trade-offs.

The Bartlett Window

The Bartlett window of length 21,

wBartlett,21[n]wBartlett,21[n]

, is shown in Figure (2). Unlike the rectangular window, the Bartlett has a smoother transition from zero to one and vice versa.

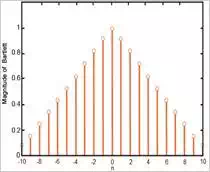
Figure (2) The Bartlett window for

M=21M=21

In order to calculate the Fourier transform of the Bartlett window, we can consider Figure (2) as the convolution of two rectangular windows of length 11,

wRectangular,11[n]wRectangular,11[n].

Of course, we will need to consider a magnitude scaling for these two rectangular windows to have the Bartlett window of Figure (2) after convolving the rectangular windows. In this example, the scaling factor is

111−−√=0.3015111=0.3015

. This rectangular window is shown in Figure (3).

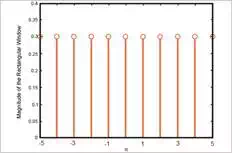
Figure (3) The rectangular window with the appropriate length and height to calculate the Fourier transform of a Bartlett window with

M=21M=21

Therefore, we obtain

wBartlett,21[n]=(111−−√wRectangular,11[n])∗(111−−√wRectangular,11[n])wBartlett,21[n]=(111wRectangular,11[n])∗(111wRectangular,11[n])

Equation (1)

We know that convolution in time domain is equal to multiplication in the frequency domain, hence

WBartlett,21(ω)=111(WRectangular,11(ω))2WBartlett,21(ω)=111(WRectangular,11(ω))2

Equation (2)

With an odd

MM

, it can be shown that

WBartlett,M(ω)=2M+1(WRectangular,M+12(ω))2WBartlett,M(ω)=2M+1(WRectangular,M+12(ω))2

Equation (3)

where

WRectangular,M(ω)WRectangular,M(ω)

is given by Equation (5) of the previous article as:

WRectangular,M(ω)=⎧⎩⎨sin(ωM2)sin(ω2)Mω≠0ω=0⎫⎭⎬WRectangular,M(ω)={sin(ωM2)sin(ω2)ω≠0Mω=0}

Equation (4)

Equation (3) reveals the most important properties of the Bartlett window:

1. Main lobe width of a Bartlett window: The roots of a Bartlett window of length

2. MM

3.  are the same as the roots of a rectangular window of length

4. M+12M+12

5.  which are at

6. 4kπM+14kπM+1

7.  where

8. kk

9. is an integer. Therefore, the main lobe width of a Bartlett window is almost twice the main lobe width of a rectangular window. In other words, since compression in the time domain corresponds to expansion in the frequency domain and any Bartlett is related to a rectangular window of half its length, we expect that the main lobe width of a Bartlett window of length

10. MM

11. will be twice the main lobe width of a rectangular window of the same length.

12. The PSL of a Bartlett window: In order to compare the PSL of a Bartlett with that of a rectangular window, consider the normalized Fourier transform of the rectangular window as shown in Figure (1). In this figure, the magnitude of the first sidelobe is about 0.22 which, considering the normalized magnitude, gives a PSL of

13. 20log(0.22)≈−13dB20log(0.22)≈−13dB

14. . Since the Fourier transform of the Bartlett is equal to the square of the Fourier transform of the rectangular window, the PSL of a Bartlett window will be

15. 20log(0.222)≈−26dB20log(0.222)≈−26dB

16. . Expressed in decibels, the PSL of a Bartlett window is reduced by a factor of 2 relative to that of a rectangular window.

Figure (4) shows the Fourier transform of a Bartlett window with

M=21M=21

which is plotted by MATLAB.

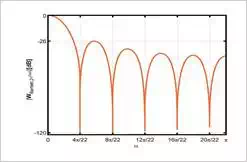
Figure (4) The magnitude of the Fourier transform of a Bartlett window with

M=21M=21.

The above discussion shows a trade-off between the main lobe width and PSL. Therefore, we can use a Bartlett window with an appropriate length,

MM

, to simultaneously reduce the PSL and main lobe width.

At this point, the reader may wonder if there is a window which can provide a better performance than that of a Bartlett in terms of main lobe width and PSL? Is there an optimum or a near-optimum window for a fixed

MM

?

Summary

● To reduce the PSL, we can try different window types such as the rectangular, Bartlett, etc.

● Window type and the window length are the two parameters that determine the main lobe width.

● We usually search for a window type which has the acceptable PSL and then choose

● MM

● long enough so that the main lobe width decreases to an acceptable value too.

● The main lobe width of a Bartlett window of length

● MM

● is twice the main lobe width of a rectangular window of the same length.

● Expressed in decibels, the PSL of a Bartlett window is reduced by a factor of 2 relative to that of a rectangular window.