Characteristics of
Junction Diodes
In this
article, we will look at the characteristics of junction diodes and learn how
to analyze circuits containing diodes that
operate in the forward, reverse, and breakdown biases.
Junction Diode Characteristics
One of the most common
applications of the diode is the pn junction.
This pn junction can be used to operate and
implement the functions of a diode because it can conduct considerable current
in the forward direction and roughly no current in the reverse direction. In
this article, we will focus on the i-v characteristics of the junction
diode, specifically the pn junction.
Figure 1.1 illustrates the
characteristics of a silicon junction diode. This same diode and its
characteristics are shown in Figure 1.2 to illustrate more of the diode's
properties. Looking at Figure 1.2, note that there is a discontinuity at the
origin; this discontinuity is caused by having a change of scales from the
reverse and forward voltage. The characteristic curve of the pn junction is made of three unique regions:
1. The forward bias region - this is
determined by v > 0
2. The reverse bias region - this is
determined by v < 0
3. The breakdown region - this is determined by v <
-VZK
We'll learn about each of
these regions, starting with the forward bias region.
Forward Bias Region
The forward bias region
begins operation when the terminal voltage is positive. In this region, the i-v relationship can be
characterized by:
i=IS(ev/VT−1)i=IS(ev/VT−1)
Equation 1.1
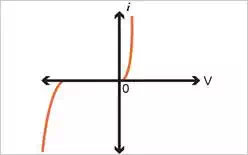
Figure 1.1 Characteristics of a silicon
junction diode
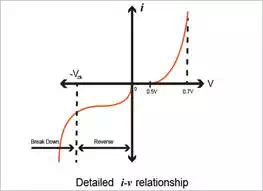
Figure 1.2 Details of the diode's relationship
between current and voltage
In Equation 1.1, IS is a
constant value that is given to a specific diode at a given temperature. This
current, IS, is known as the saturation current.
Alternatively, another name that is more commonly used is the scale current.
This scale reference name arose from the current, IS, being directly proportional to the
cross-sectional area of the given junction diode. With this in mind, if the
area of the junction diode is doubled, the value of IS is consequently
doubled.
As for small-signal diodes,
which are very commonly used in electronic circuits where a high frequency or
small current is required (such as televisions, radio, and digital logic circuits), Is is generally on the
order of 10-15 Amps. The scale current is
considered to be a strong function of temperature and doubles for every 5ºC
rise in temperature.
If we look at Equation 1.1
again, the voltage, VT, is known as the thermal voltage, which is a constant
given by:
VT=kTqVT=kTq
Equation 1.2
and
● k = Boltzmann's constant = 1.38•10-23 joules/kelvin
● T = Absolute temperature given in
kelvins = 273.15 + temperature in ºC
● q = Electric charge magnitude = 1.60•10-19 coulombs
Then If we
substitute the Boltzmann's constant into Equation 1.2, we get:
kq=1.381⋅−23JK1.602⋅−19C=86.2μVKkq=1.381⋅−23JK1.602⋅−19C=86.2μVK
Equation 1.2a
and since by definition 1 V = 1 J/C,
we are provided with
VT=(86.2μVK)TVT=(86.2μVK)T
If we consider room
temperature (20ºC), Equation 1.2a provides a voltage value for VT of 25.3 mV.
If we look at the junction
diode that operates in the forward direction with current i (more so for i >> IS), then Equation 1.1 can be estimated
by an exponential relationship of the voltages:
i≃ISev/VTi≃ISev/VT
Equation 1.3
This same equation can be
written in a logarithmic form alternatively as
v=VTlniISv=VTlniIS
Equation 1.4
This exponential relationship
is an extraordinary characteristic of junction diodes and has been used to
found many in many fascinating applications.
Looking now at the forward
bias i-v relationship found
in Equation 1.3, we can evaluate the current I1 that has a corresponding diode
voltage of V1 to
be
I1=ISeV1/VTI1=ISeV1/VT
Equivalently, if we have a
diode voltage of V2, we
will have a diode current of I2 given by
I2=ISeV2/VTI2=ISeV2/VT
Thus, we can combine these
two equations to give
I2I1=e(V2−V1)/VTI2I1=e(V2−V1)/VT
which, by simplifying, provides
V2−V1=VTlnI2I1V2−V1=VTlnI2I1
Looking closely at Figure
1.2, we see that the current is rather small for v smaller
than 0.5 v, which we consider to be negligible. This voltage value is
referenced as the cut-in voltage. This is the definite forward voltage where
the diode begins to conduct significantly. This threshold in the
current-voltage characteristic is a consequence of the exponential relationship.
Another consequence of this
relationships causes the rapid increase in the current i.
Furthermore, for a diode that is said to be "fully conducting", the
voltage drop is found in a rather narrow range, roughly 0.6 to 0.8 V. This
provides a simple model for the diode as we assume that the conducting diode
has a voltage of approximately 0.7 V across it. There are many different diodes
which will exhibit this same 0.7 V drop, but at different current values. For
example, if we consider a small-signal diode, a voltage drop of 0.7 V will be
at i = 2 mA, while a larger power
diode may have this same 0.7 V drop at i =
2 A.
Reverse Bias Region
This region begins its
operation when the diode's voltage, v, goes to a negative
value. The very first equation discussed in this article, Equation 1.1,
illustrates that, if the voltage is negative and slightly larger than VT (~25.3 mV), then the exponential
term,
vVTvVT
, is trivial when compared to the whole. Thus the diode's current can be expressed as:
i≃−ISi≃−IS
What this means is that, if
the current is in the reverse direction, it is considered to be constant and
equivalent to IS.
Because this current is consistent, it earned the name "saturation
current".
However, real diodes do
exhibit these reverse currents and while they may be relatively small, are much
larger than IS. For
example, if we look at a small signal diode's saturation current that is said
to be 10-14 to 10-15 A, it could exhibit a reverse
current of 1 nA. This current will increase
partially with the increase in magnitude of the reverse voltage. Due to the relatively
small magnitude of the reverse current, it is not possible to see the
current-voltage characteristic on Figure 1.2.
Breakdown Region
The last region of diode
operation is known as the breakdown region, which is illustrated in Figure 1.2.
This region is entered only when the magnitude of the reverse voltage surpasses
a threshold value that is pertinent to the particular diode itself, known as
the breakdown voltage. This is also known as the "knee" of the
current-voltage curve in Figure 1.2, which is labeled as VZK, where Z denotes zener and K stands for knee.
As we look at the detailed
figure illustrating the current-voltage characteristics, we see that the
reverse current increases drastically in the breakdown region, while the
voltage drop is rather small. A diode breakdown is typically not destructive,
granted that the power that is dissipated within the diode is restricted by an
external circuit at a safe level. This level is usually specified on the device
or in the device's manual. Thus, it is necessary to restrict the reverse
current in this breakdown region to a specific value that is consistent with
the allowed power dissipation.
One more thing worth noting
is that, because the current-voltage characteristic in the breakdown region is
very close to a vertical line, we can use it in voltage regulation
applications. We will discuss this in a separate article.
Conclusion
In this article, we discussed
the three different regions of a junction diode and their characteristics. I
hope that this article has helped you attain a better understanding of junction
diodes. You should be able to differentiate between each region, as well as be
able to explain what they are used for.
In the next article, we will
delve more specifically into the forward direction and the
constant-voltage-drop model. Building upon the previous articles in this
series, we will now be able to talk about the analysis of circuits that utilize
forward conduction diodes.
Thank you for reading. If you
have any questions or comments, please leave them below!