Non-inverting
Configuration of an Operational Amplifier
Learn about
non-inverting amplifiers.
Mentioned in the previous
article, the first of two most commonly used operational amplifiers, the
inverting configuration is heavily used in audio mixers or digital-to-audio
converters. In this article, we will discuss the second amplifier configuration,
known as the non-inverting amplifier.
Non-inverting Configuration
The second closed-loop
configuration of an operational amplifier that we'll be talking about in this
series of articles is that of a Non-inverting Operational Amplifier and is
shown in Fig. 1. In this configuration, the input signal v1 is applied right
into the positive terminal (or non-inverting terminal) of the operational
amplifier and at the negative terminal (or inverting terminal), a resistor R1
is connected to ground. This means that the output gain of the operational
amplifier is changed to "positive" in value; on the other hand in the
inverting amplifier, we saw that the output gain is negative in value. From
this, we see that this will result in the output signal being in phase with the
input signal.
Closed-Loop Gain
By analyzing the
non-inverting circuit, we can determine its closed-loop gain (v0/v1) and is
illustrated in Figure 1.2. The order of operation and procedure is labeled by boxed numbers on the figure. Suppose that
the operational amplifier is considered to be ideal with an infinite gain, we
see that there is a "virtual short circuit" that exists between the
inverting and non-inverting input terminals. The difference in the input signal
can be noted as
vid=v0A=0vid=v0A=0
for
A=∞A=∞
Put into words, at the
inverting input terminal, the voltage will be equivalent to the voltage value
that is currently at the non-inverting input terminal, known as the applied
voltage v1. A current that flows through R1 can thus be described as v1/R1. Due
to the fact that the (ideal) operational amplifier has an infinite input
impedance, the current through R1 will flow through R2 as well. We can now
calculate for the output voltage from
v0=v1+(v1R1)R2v0=v1+(v1R1)R2
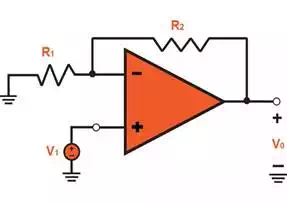
FIGURE 1.1: Noninverting Configuration
Which provides
v0v1=1+R1R2v0v1=1+R1R2
(Eq. 1.1)
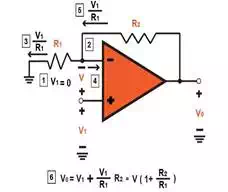
FIGURE 1.2
Also, by inspecting the
non-inverting configuration further we can see how it operates. Because of the
current that flows directly into the operational amplifier's inverting terminal
is zero, the two resistors R1 and R2 act as a voltage divider that allows a
small portion of the output voltage to loop back to the inverting input
terminal. This is written by
v1=v0(R1R1+R2)v1=v0(R1R1+R2)
(Eq 1.2)
Thus, the infinite gain and
the "virtual short circuit" produced that is located between the
inverting and non-inverting terminals of the operational amplifier will force
the voltage to be equivalent to the voltage applied at the non-inverting input
terminal. Then,
v0(R1R1+R2)=v1v0(R1R1+R2)=v1
Which provides the
operational amplifier's gain expression in equation 1.1.
We will stop to notice the
presence and the action of the negative feedback that arises in the
non-inverting configuration of Fig 1.1. By letting v1 increase, vid will
increase consequently, and v0 will correspondingly increase due to the high
gain of the (ideal) operational amplifier. However, when v0 is correspondingly
increased, a small fraction is fed back into the inverting input terminal
through the two resistors (or voltage divider). This feedback's purpose is to
counteract the voltage increase in vid, and push it down to zero, although it
is a higher value of v0 that does indeed correspond to the increase in v1. This
is what is known as a degenerative action, thus, the feedback is given the name
of degenerative feedback.
Finite Open-Loop Gain Effects
Just as was done for the
inverting configuration, we will now take a look at the effects of the finite
operational amplifier open-loop gain A on this configuration. By assuming the
operational amplifier to be all ideal expect for the open-loop gain A, we can
show that the closed-loop gain of the non-inverting configuration by
G=v0v1=1+(R2/R1)1+1+(R2/R1)AG=v0v1=1+(R2/R1)1+1+(R2/R1)A
(Eq. 1.3)
It is of importance that for
both configurations, inverting and non-inverting, the denominator of Eq. 1.3 is
identical. This is because of the fact that both the configurations have the
same exact feedback loop, which can easily be seen if the input signal source
is short-circuited. It is only the denominators that are identical because the
numerators give the ideal closed-loop gain (-R2/R1 for inverting and 1 + R2/R1 for non-inverting). One more thing to note is that the
gain expression in Eq. 1.3 can be simplified and thus give the ideal value for
A=∞A=∞
Resistance
The gain A of
this configuration is positive, hence, why it is called non-inverting.
Looking at the input, the impedance of the closed-loop amplifier is ideally
infinite, due to no current flowing into the noninverting input terminal of the
operational amplifier. Now, looking at the other end, the output is to be taken
at the terminals of the voltage source
A(v2−v1)A(v2−v1)
, thus leaving the output resistance of the non-inverting configuration to
be zero.
Voltage Follower
The high input impedance has
a property that plays a key role of the noninverting configuration. This
impedance allows the circuit to be used as a buffer amplifier that connects to
a source that goes from a high to low impedance load. In many instances, the
applications that use buffer amplifiers are not required to provide any voltage
gain. Rather, it is used as an impedance transformer or a power amplifier
instead. In these applications R2=0 and
R1=∞R1=∞
to provide for the unity-gain
amplifier shown in Fig 1.3 (a). This circuit is commonly known as the voltage
follower. This is known as a follower as the output follows the input's
voltage. Speaking of the ideal case, v0=v1,
Rin=∞Rin=∞
,
Rout=0Rout=0
, and the circuit is shown in Fig 1.3 (b).
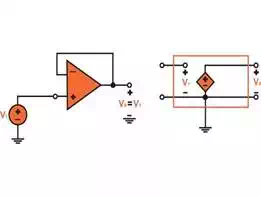
FIGURE 1.3 (a) (b)
Due to the fact that the
voltage follower circuit's entire output is fed back directly into inverting
input, the circuit is now said to have 100% negative feedback. The infinite
gain of the ideal operational amplifier will now act to ensure that vid=0 and thus v0=v1.
Conclusion
To conclude this article, the
non-inverting configuration has been discussed and explained. I hope that you
have gained a better understanding of the purpose of this amplifier as well as
how it is operated. Whether it is a buffer amplifier or impedance transformer,
you'll find a non-inverting amplifier within it. Two things are to be
remembered when discussing non-inverting amplifiers: no current flows through
the noninverting input terminal and that the input signal is applied to the
non-inverting terminal. From these two rules, we derived an equation to
calculate the closed-loop gain of the non-inverting amplifier. If you have any
questions or comments, please leave them below!