Everything About the Quine-McCluskey Method

In order to accurately use the Quine-McCluskey, the function needs to be given as a sum of minterms (if the Boolean function is not in minterm form, the minterm expansion can be found) to determine a minimum sum-of-products (SOP) expression for a function. During the first step of the method, all prime implicants of a function are systematically formed by combining minterms. These minterms are represented in a binary notation and combined as follows:

XY + XY’ = X             (1.1)                                                       

where X is represented by a product of literals and Y is a single variable of some sort. If two variables differ in exactly one variable, the two minterms will combine together.

To find all prime implicants, all possible pairs of minterms should be compared and combined whenever possible. Sorting binary minterms into groups according to the number of 1’s in each term, reduces the required number of comparisons one must complete. Thus.

f(a,b,c,d)=∑m(0,1,2,5,6,7,8,9,10,14)f(a,b,c,d)=∑m(0,1,2,5,6,7,8,9,10,14)

                        (1.2)

can be represented by the list of minterms below:

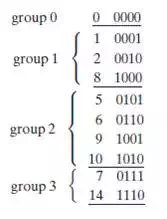
In this list, the term in group 0 has zero 1’s, group 1 terms have one 1, group 2 has two 1’s, and finally group 3 has three 1’s. Any two terms can be combined if the difference is only one variable. If two terms are compared in nonadjacent groups, there is no need for comparing as such terms will always differ in two variables; they also cannot be combined using XY + XY’ = X. Likewise, comparing terms within a group is not necessary because each term will have the same amount of 1’s and do not differ by at least two variables. With that being said, terms in adjacent groups only need to be compared.

Always start with group 0. First, the group 0 term will be compared with all terms in group 1. The 0000 and 0001 terms can be combined to eliminate the fourth variable in both terms, which produces 000-. Comparably, 0 and 2 (0000 and 0010) combine to form 00-0 (or a’b’d’), and 0 and 8 (0000 and 1000) combine to form -000 (or b’c’d’). The resulting terms are listed in the table below.

No matter when two terms are combined, the corresponding decimal numbers differ by a power of 2. This statement holds true because when the binary representations differ in exactly one column. If these binary representations are subtracted, a difference of exactly 1 is found in the column in which the difference exists.

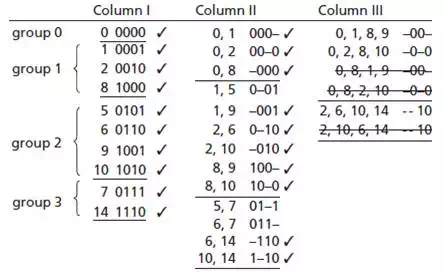
Comparing group 0 with group 2 or 3 is quite unnecessary because there will be a difference of more than one variable, thus proceeding to the next step of the method. When comparing term 1 (0001) in group 1 with all of group 2’s terms, terms 5 and 9 (0011 and 1001) can be combined but not 6 or 10 (0110 or 1010). The reduced terms (0-01 and -001) are moved to column II. Once a term has been combined with another term, a check is placed next to it, signifying that the term has been used in a simplification already. Likewise, term 2 in group can only combine with 6 and 10, and term 8 of group only combines with 9 and 10. A term may be used to combine with another term more than once because X + X = X. If two terms have already been combined with other terms, they must still be compared and combined if possible. This is necessary to provide a preferred simplification of a minimum sum solution. To finish comparison in column I, all terms in groups 2 and 3 are compared and simplified if possible. By combining terms 5 and 7, 6 and 7, 6 and 14, and 10 and 14, new terms are placed in column II.

Just like in column I, the terms are divided amongst groups pertaining to the amount of 1’s in each term. Once again XY + XY’ = X is applied to find combinable pairs in column II. In this column the terms must have the same variables and the terms must differ by only one variable. First group terms in column II only need to be compared with terms in the second group which have dashes in the same place. The term 000- (terms 0 and 1 combined) can only be combined with the term 100- (terms 8 and 9 combined) to provide a combined term of -00-. This equates algebraically to a’b’c + ab’c’ = b’c’. This combined term is thus placed in column III denoted for 0,1,8,9 indicating that it was formed by comparing those minterms. Term (0, 2) can combine only with (8, 10) and the term (0, 8) with (1, 9) and (2, 10). Next, comparing terms in groups 2 and 3, (2, 6) can be combined and simplified with (10, 14), as well as (2, 10) with (6, 14). These terms can now be checked off in column II as they have been used to simplify the Boolean function.

The three terms left in column III are duplicate terms and were formed by combing the same set of four minterms in a different order. Since there are no further possible simplifications of any terms, the Quine-McCluskey process is complete. If there were more terms available for combinations, the comparison and simplification process would be continued, forming more groups and columns until all terms weren’t able to be combined.

Looking at chart, some terms have not been checked off; this is because they cannot possibly be combined with other terms, these terms are called prime implicants. Since every minterm has been included with at least one prime implicants, the function is now equal to the sum of its prime implicants. For example,

f = a’c’d + a’bd + a’b’c +                              b’c’ +               b’d’ +              cd’

                    (1, 5)  (5, 7)  (6, 7)                    (0, 1, 8, 9)   (0, 2, 8, 10) (2, 6, 10, 14)                     (1.3)

The expression above has a minimum number of literals. A literal is a simple variable within a term which may or may not be complemented. The number of terms, however, is not minimum. By using the consensus theorem redundant terms can be eliminated as follows

f = a’bd + b’c’ + cd’               (1.4)

this is the minimum SOP expression for f. A follow up article will delve into a more efficient for eliminating redundant prime implicants using what’s known as a prime implicants chart.

To relate and understand what a implicant and prime implicant is when related to with the Quine-McCluskey method, they will be defined. Given a function F of n variables, a product term P is an implicants of F if and only if for every combination of values of the n variables for which P = 1, and F is also equal to 1. A prime implicant of a function F is a product term implicants which is no longer an implicants if any literal is deleted from it. 

Coming Up

As previously illustrated, the Quine-McCluskey method find all of the product term implicants of a Boolean function. At this point, you should have an understanding of what a prime implicant is and how to find one by using the Quine-McCluskey method. Also given the prime implicants, essential prime implicants and a minimum SOP expression should be able to be found. Future articles will talk about the prime implicant chart, Patrick’s Method, and simplification of incompletely specified functions.