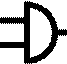
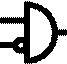
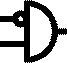
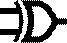Universal Logic Gates
Introduction
A universal logic gate is a
logic gate that can be used to construct all other logic gates. There
are many articles about how NAND and NOR are universal gates, but many of these
articles omit other gates that are also universal gates. This article covers
two input logic gates, demonstrates that the NAND gate is a universal gate, and
demonstrates how other gates are universal gates that can be used to construct
any logic gate.
Two Input Logic Gates
For 2 logical inputs, there
are 16 possible logic gates. Table 1 defines the 16 logic gates, shows logical
symbol, behavior in symbolic logic,
provides name, notes.
People are most familiar with
the ones that are named: NAND, NOR, AND, OR, XOR. Table 1 includes these, as
well as AND and OR gates with either input
negated, logic 0 and logic 1(which aren't
really logic gates), and some gates that aren't really binary.
|
|
Output when AB is |
|
|
|
|
|||
|
Gate # |
00 |
01 |
10 |
11 |
Symbolic Logical Description |
Symbol |
Name/Description |
Note |
|
0 |
0 |
0 |
0 |
0 |
0 |
|
Always zero |
Not really a gate |
|
1 |
0 |
0 |
0 |
1 |
A & B |
|
AND |
|
|
2 |
0 |
0 |
1 |
0 |
A & ~B |
|
A and Not B |
Universal |
|
3 |
0 |
0 |
1 |
1 |
A |
|
A |
Not Binary |
|
4 |
0 |
1 |
0 |
0 |
~A & B |
|
B and Not A |
Universal |
|
5 |
0 |
1 |
0 |
1 |
B |
|
B |
Not Binary |
|
6 |
0 |
1 |
1 |
0 |
(A & ~B) | (~A & B) |
|
XOR |
Also Not Equals Function |
|
7 |
0 |
1 |
1 |
1 |
A | B |
|
OR |
|
|
8 |
1 |
0 |
0 |
0 |
~(A | B) |
|
NOR |
Universal |
|
9 |
1 |
0 |
0 |
1 |
(A & B) | (~A & ~B) |
|
XNOR |
Also Equals Function |
|
10 |
1 |
0 |
1 |
0 |
~B |
|
Not B |
Not Binary |
|
11 |
1 |
0 |
1 |
1 |
A | ~B |
|
A or Not B |
Universal |
|
12 |
1 |
1 |
0 |
0 |
~A |
|
Not A |
Not Binary |
|
13 |
1 |
1 |
0 |
1 |
~A | B |
|
B or Not A |
Unversal |
|
14 |
1 |
1 |
1 |
0 |
~(A & B) |
|
NAND |
Universal |
|
15 |
1 |
1 |
1 |
1 |
1 |
|
Always 1 |
Not really a gate |
Table 1: 2 Input Logic Gates
NAND Gate is a Universal Gate
NAND gates can be connected
to form any other logic gates. Figures 1,2,3 show
how NAND gates can be connected to form INVERTER, AND, and OR gates. These
gates can be combined to form the other logic gates according to the symbolic
logic definitions in table 1.
Figure 1:
Connecting a NAND gate to make an INVERTER gate
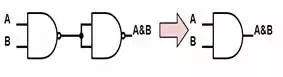 Figure 2: Connecting NAND gates to make
an AND gate
Figure 2: Connecting NAND gates to make
an AND gate
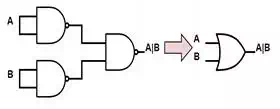 Figure 3: Connecting NAND gates to make
an OR gate
Figure 3: Connecting NAND gates to make
an OR gate
Other Universal Gates
Gates 2,4,11, and 13 are
universal gates. To prove this, we demonstrate building NAND gates with these
gates. Gates 7 and 8 are the same gate but with different inputs inverted.
Gates 9 and 10 are the same gate but with different inputs inverted. Proving
that gates 2 and 11 are universal is enough to prove that gate 4 and 13 are
universal as well.
Gate 11: A | ~B
Figures 4 and 5 show show gate 11 can be combined to create INVERTER
and AND gates. INVERTER and AND gates can be connected in series to construct a
NAND gate. Because gate 11 can be used to construct a NAND gate, and a NAND
gate is a universal gate, gate 11 is a universal gate. Since gates 11 and 13
are mirrors of each other, gate 13 is also a universal gate.
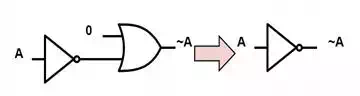 Figure 4: Connecting gate 11(A |~B) to
create an INVERTER gate.
Figure 4: Connecting gate 11(A |~B) to
create an INVERTER gate.
 Figure 5: Connecting gate 11(A |~B) to
create an AND gate. There may be a way to do this with fewer gates. The figure
here is the one the author could derive the quickest.
Figure 5: Connecting gate 11(A |~B) to
create an AND gate. There may be a way to do this with fewer gates. The figure
here is the one the author could derive the quickest.
Gate 2: A & ~B
Figures 6 and 7 show show gate 2 can be combined to create INVERTER
and AND gates. INVERTER and AND gates can be connected in series to construct a
NAND gate. Because gate 2 can be used to construct a NAND gate, and a NAND gate
is a universal gate, gate 2 is a universal gate. Since gates 2 and 4 are
mirrors of each other, gate 4 is also a universal gate.
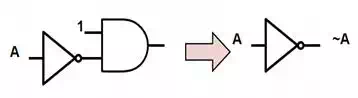 Figure 6: Connecting gate 2(A &~B)
to create an INVERTER gate.
Figure 6: Connecting gate 2(A &~B)
to create an INVERTER gate.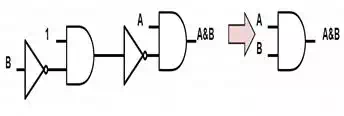 Figure 7: Connecting gate 2(A &~B)
to create an AND gate.
Figure 7: Connecting gate 2(A &~B)
to create an AND gate.
Conclusion
This article has discussed
logic gates, universal gates, demonstrated that the NAND gate is a universal
gate, and proven that four additional universal logic gates exist. This is an
interesting academic exercise. In practice, the author would recommend sticking
to using NAND gates as universal gates because they are so cheap and small to
construct, or if doing board level design using chips with the actual gates
that are wanted and not using universal gates.