Boolean Identities
The main
identities associated with Boolean algebra.
Prerequisite
Reading
This article assumes that you
have read and are comfortable with the Boolean Basics article
(which also contains a list of links to other articles in this series). If you
find yourself having difficulty following the concepts or notation used here,
you might review that article.
Boolean Identities- Summary
Like normal algebra, Boolean
algebra has a number of useful identities. An "identity" is merely a
relation that is always true, regardless of the values that any variables
involved might take on. Many of these are very analogous to normal multiplication
and addition, particularly when the symbols {0,1} are
used for {FALSE,TRUE}. But while this can be useful, there are some identities
that are different and that cause confusion for many people -- we will
highlight these as we encounter them. We begin with a table summarizing these
identities and then proceed to examine each of them in detail.
|
IDENTITY |
EXPRESSION |
|
|
Logical Inverse |
0ŻŻŻ=1;1ŻŻŻ=00Ż=1;1Ż=0 |
|
|
Involution |
AŻŻŻŻŻŻŻŻ=AAŻŻ=A |
|
|
|
OR |
AND |
|
Dominance |
A+1=1A+1=1 |
A⋅0=0A⋅0=0 |
|
Identity |
A+0=AA+0=A |
A⋅1=AA⋅1=A |
|
Idempotence |
A+A=AA+A=A |
A⋅A=AA⋅A=A |
|
Complementarity |
A+AŻŻŻŻ=1A+AŻ=1 |
A⋅AŻŻŻŻ=0A⋅AŻ=0 |
|
Commutativity |
A+B=B+AA+B=B+A |
A⋅B=B⋅AA⋅B=B⋅A |
|
Associativity |
(A+B)+C=A+(B+C)(A+B)+C=A+(B+C) |
(A⋅B)⋅C=A⋅(B⋅C)(A⋅B)⋅C=A⋅(B⋅C) |
|
Distributivity |
A+(B⋅C)=(A+B)⋅(A+C)A+(B⋅C)=(A+B)⋅(A+C) |
A⋅(B+C)=(A⋅B)+(A⋅C)A⋅(B+C)=(A⋅B)+(A⋅C) |
|
Absorption |
A⋅(A+B)=AA⋅(A+B)=A |
A⋅(A+B)=AA⋅(A+B)=A |
|
DeMorgan's |
A+B=AŻŻŻŻ⋅BŻŻŻŻŻŻŻŻŻŻŻŻŻŻŻA+B=AŻ⋅BŻŻ |
A⋅B=AŻŻŻŻ+BŻŻŻŻŻŻŻŻŻŻŻŻŻŻŻŻŻŻA⋅B=AŻ+BŻŻ |
Each of these identities can
be proven by simply creating a fully-enumerated truth table for the expression
on the left (of the equality sign, not of the table) and another for the
expression on the right and showing that they produce the same result for every
possible input combination. This will be done for each identity. A more elegant
way is to use previously proven identities to prove subsequent ones. In general
we will not do this primarily because the ordering of the table above is
intended to follow a largely intuitive progression and it is not optimized for
supporting a chain of Boolean proofs.
Notice that for each identity
involving the OR and/or the AND operator, there is a corresponding identity in
which the roles of these two operators are reversed. This is due to the
"duality" of AND and OR, a topic
explored in detail in a separate article.
In all of the expressions in
this article we make no assumption about either the precedence or the
associativity of the operators, meaning that we will rely heavily on fully
parenthesized expressions. Because we will use the overbar notation for logical
negation (the NOT operator), we will use the natural convention that the
expression underneath the bar is evaluated and the result of that is then
inverted (NOTed).
Boolean Identities- Detailed Explanations
We will now work our way
through the table of identities, in order, making observations about each,
usually including a "common sense" informal proof. In addition to the
Boolean expressions, each identity will also be depicted graphically using
standard logic schematic symbols. The symbols for NOT, OR, and AND were introduced in the Boolean Basics article. In
addition to these, we will use the BUF symbol to represent a non-inverting
buffer. This gate merely copies its input to its output. Furthermore, while we
use {0, 1} to represent {FALSE, TRUE} in the Boolean expressions, we will use
{LO, HI} to represent them in the schematic diagrams.
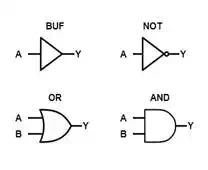
Notice that the NOT symbol is
simply a BUF symbol followed by a bubble. The bubble represents logical
inversion and is the actual NOT gate. Anytime you see a bubble attached to a
gate pin, you can detach it from the pin and insert a separate NOT gate in its
place without affecting the resulting logic.
Each discussion is followed
by a formal proof via fully-enumerated truth tables. For most of the
identities, these proofs will not contain any suprises.
But they are worthwhile including because some of the less-intuitive proofs
might make more sense when you can see how the logic progresses through the
tables.
Logical Inverse
This identity, which is
actually two separate identities, is merely the definition of logical negation
applied to each of the possible Boolean values.
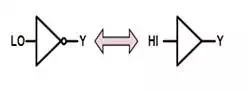
0ŻŻŻ=10Ż=1
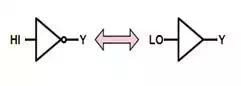
1ŻŻŻ=01Ż=0
Proof
Since this is our first
identity, our proof must be based on the fundamental definitions of the signals
and the operators (which will be true of several early identities). As the only
operation involved here is negation, we simply site the definition of negation
and note that these identities are simply the two rows in that definition.
|
0 |
LHS 0ŻŻŻ0Ż |
RHS 1 |
|
0 |
1 |
1 |
|
1 |
LHS 0ŻŻŻ0Ż |
RHS 0 |
|
1 |
0 |
0 |
Involution
In mathematics, a function is
said to be involutive if it is its own
inverse. In normal arithmetic, the reciprocal function is involutive since the reciprocal of a reciprocal yields
the original value, as does multiplying a value twice by -1. In Boolean logic,
negation is aninvolutive function because negating
a value twice returns the original value. This is analogous to the "double
negative" in normal conversation.
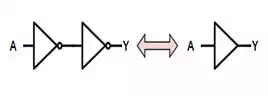
AŻŻŻŻŻŻŻŻ=AAŻŻ=A
or
(A′)′=A(A′)′=A
PROOF
|
A |
AŻŻŻŻAŻ |
(AŻŻŻŻ)ŻŻŻŻŻŻŻŻŻŻ=AŻŻŻŻŻŻŻŻ(AŻ)Ż=AŻŻ |
LHS AŻŻŻŻŻŻŻŻAŻŻ |
RHS A |
|
0 |
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
1 |
Dominance
In normal multiplication, we
have the property that anything multiplied by zero yields zero. In a sense,
this means that zero has the ability to suppress, mask, or dominate any other
value under multiplication. The dominance identity -- also known the "suppression"
or "masking" identity -- is similar and merely recognizes that
anything that is OR'ed with a TRUE produces
a TRUE while anything AND'ed with a FALSE
produces a FALSE.
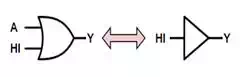
A+1=1A+1=1

A⋅0=0A⋅0=0
While the second property
looks the same as normal multiplication, the first property is definitely NOT
the same as normal addition. This is something to keep in mind until you are
proficient with Boolean algebra because it is very easy to fall back on
well-entrenched habits and apply rules from normal algebra to Boolean algebra
when they simply aren't valid, or fail to exploit rules that are.
PROOF
|
A |
1 |
LHS A+1 |
RHS 1 |
|
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
|
A |
0 |
LHS A⋅0A⋅0 |
RHS 0 |
|
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
Note that, technically, the
proofs given here only apply to the case when the first input is the free
variable and the second input is the dominant value for that operation. We
could prove that the identity holds with the inputs are swapped, but once we prove
that both OR and AND are commutative, those
proofs become trivial and uninteresting.
Identity
Just as 0 is the identity
element for normal addition and 1 is the identity element for multiplication,
so too are 0 (FALSE) and 1 (TRUE) the identity elements for OR and AND respectively.
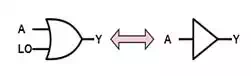
A+0=AA+0=A
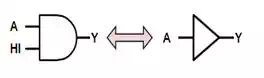
A⋅1=AA⋅1=A
This property, more than
anything else, is why the addition symbol is used for logical OR and the
multiplication symbol is used for logical AND. But it is important to remember
that, in Boolean algebra, we are NOT "adding" or "multiplying"
two values to when we use these operators. Using this terminology is poor form
and generally frowned upon (even though it is heard quite regularly). Having
said that, the terms "sum" and "product" are widely used
and accepted for the results of logical OR and logical AND, respectively. So
while it is poor form to talk about "adding A and B," it is
acceptable to talk about "the sum of A and B"; this may seem odd and
even inconsistent, but it is simply the result of a compromise that has evolved
between mathematically rigorous terminology and practical common parlance --
for instance, it is easier and cleaner to speak of "the sum of
products" than is "the OR of ANDs".
The identity for OR comes
directly from the definition of OR when the second input is constrained to be
0, while the identity for AND comes directly from it's definition
when the second input is constrained to be 1.
PROOF
The identity for OR comes
directly from the definition of OR when the second input is constrained to be
0, while the identity for AND comes directly from it's definition
when the second input is constrained to be 1.
|
A |
0 |
LHS A+0 |
RHS A |
|
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
A |
1 |
LHS A⋅1A⋅1 |
RHS A |
|
0 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
Note that, technically, the
proofs given here only apply to the case when the first input is the free
variable and the second input is the identity value for that operation. We
could prove that the identity holds with the inputs are swapped, but once we prove
that both OR and AND are commutative, those
proofs become trivial and uninteresting.
Idempotence
The term
"idempotent" describes an operation that can be carried out any
number of times and the effect is the same as if it had only been carried out
once. If we either AND a Boolean variable with itself or OR it with itself, we get the same result as the
original variable. This means that both AND and OR
are idempotent. This property is expressed as
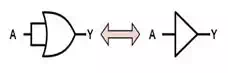
A+A=AA+A=A
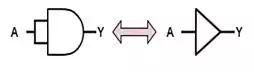
A⋅A=AA⋅A=A
Notice that this is VERY
different than normal arithmetic.
PROOF
The proof of idempotence for both OR and AND follows
from examining the definition of each operation under the constraint that both
inputs have the same value.
|
A |
A |
LHS A+A |
RHS A |
|
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
|
A |
A |
LHS A⋅AA⋅A |
RHS A |
|
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
Complementarity
A 'complement' (as opposed to
a 'compliment') is the opposite of something. In fact, another name for the
logical inverse is the complement. When we OR or AND
a Boolean value with its complement we end up with the same result regardless
of the value of the variable. In the case of AND, since we know that either the
variable or its complement FALSE, the logical AND of a variable with its
complement will always yield FALSE since the one that is FALSE will dominate.
Similarly, since we know one of them is TRUE, the logical OR of a variable with
its complement will always yield TRUE because the one that is TRUE will
dominate.
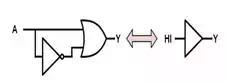
A+AŻŻŻŻ=1A+AŻ=1
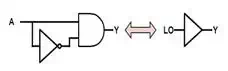
A⋅AŻŻŻŻ=0A⋅AŻ=0
To have the property of
complementarity, all that is required of a Boolean binary operator is that it
be symmetric, meaning that the two rows in its defining truth table that have
dissimilar inputs produce the same result. This is a surprisingly powerful
identity that often plays a part in reducing, or "simplifying"
Boolean expressions.
PROOF
To have the property of
complementarity, all that is required of a Boolean binary operator is that it
be symmetric, meaning that the two rows in its defining truth table that have
dissimilar inputs produce the same result.
|
A |
AŻŻŻŻAŻ |
LHS A+AŻŻŻŻA+AŻ |
RHS 1 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
1 |
|
A |
AŻŻŻŻAŻ |
LHS A⋅AŻŻŻŻA⋅AŻ |
RHS 0 |
|
0 |
1 |
0 |
0 |
|
1 |
0 |
0 |
0 |
Note that, technically, the
proofs given here only apply to the case when the first input is the uncomplemented free variable and the second input is
its complement. We could prove that the identity holds with the inputs are
swapped, but once we prove that both OR and AND are
commutative, those proofs become trivial and uninteresting.
Commutativity
As in normal arithmetic, the
order of the operands for both OR and AND do
not matter making them both commutative.
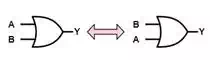
A+B=B+AA+B=B+A
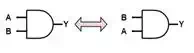
A⋅B=B⋅AA⋅B=B⋅A
This is also described by
saying that AND and OR are 'symmetric'
functions.
Like complementarity, all
that is required for a binary Boolean operator to be commutative is for the two
rows in the defining truth table having dissimilar inputs produce the same
output. The corollary to this is that any binary Boolean operator that is commutative
is also complementary, and vice verse.
PROOF
Like complementarity, all
that is required for a binary Boolean operator to be commutative is for the two
rows in the defining truth table having dissimilar inputs produce the
same ouput. The corollary to this is that any
binary Boolean operator that is commutative is also complementary, and vice verse.
|
A |
B |
LHS A + B |
RHS B + A |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
1 |
|
A |
B |
LHS A⋅BA⋅B |
RHS A⋅BA⋅B |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
|
1 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
Associativity
Again, as in normal
arithmetic with addition and multiplication, the order in which we apply
operations when two or more of the same operator are involved does not matter.
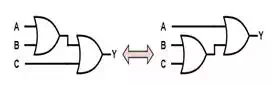
(A+B)+C=A+(B+C)(A+B)+C=A+(B+C)
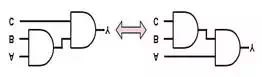
(A⋅B)⋅C=A⋅(B⋅C)(A⋅B)⋅C=A⋅(B⋅C)
The associativity of OR
and AND is not at all obvious. It is
tempting to assume that because OR and AND are
commutative that they must be associative also. This is not the case however
and some Boolean operators, NAND and NOR (discussed in a later article), that
are commutative are not associative.
PROOF
|
A |
B |
C |
(A + B) |
(B + C) |
LHS (A + B) + C |
RHS A + (B + C) |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
1 |
1 |
1 |
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
0 |
1 |
1 |
|
1 |
0 |
1 |
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
A |
B |
C |
(A⋅B)(A⋅B) |
(B⋅C)(B⋅C) |
LHS (A⋅B)⋅C(A⋅B)⋅C |
RHS A⋅(B⋅C)A⋅(B⋅C) |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
1 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
1 |
1 |
0 |
1 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Distributivity
In normal arithmetic we often
use the property that multiplication distributes over addition and are aware
that addition does not distribute over multiplication. However, in Boolean
algebra, either operator distributes over the other.
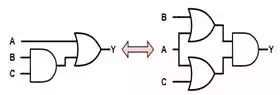
A+(B⋅C)=(A+B)⋅(A+C)A+(B⋅C)=(A+B)⋅(A+C)
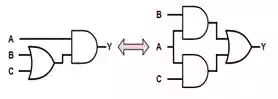
A⋅(B+C)=(A⋅B)+(A⋅C)A⋅(B+C)=(A⋅B)+(A⋅C)
This last property, because
it goes against our engrained understanding of the rules of arithmetic, seems
very unnatural and many people are unaware that it is true or actively believe
that it is not true. This is almost entirely an unintended consequence of using
the plus-sign and multiplication-sign from normal arithmetic and failing to
remember that logical operators and arithmetic operators are simply not the
same thing and that they have absolutely no relation to each other regardless
of whether we use the symbols to represent them.
Both of these properties are
extremely useful and, not suprisingly, many
people make their work much more difficult because they aren't adept at
recognizing where applying the disitributivity of
OR over AND would greatly streamline things.
PROOF
|
A |
B |
C |
(B + C) |
(A⋅B)(A⋅B) |
(A⋅C)(A⋅C) |
LHS A⋅(B+C)A⋅(B+C) |
RHS (A⋅B)+(A⋅C)(A⋅B)+(A⋅C) |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
A |
B |
C |
(B⋅C)(B⋅C) |
(A+B)(A+B) |
(A+C)(A+C) |
LHS A+(B⋅C)A+(B⋅C) |
RHS (A+B)⋅(A+C)(A+B)⋅(A+C) |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Absorption
One of the more useful
Boolean identities is absorption because it allows use to remove unneeded
variables. But, in addition, it also allows us to introduce variables that then
frequently allow us to make even greater simplifications.
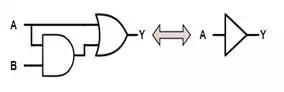
A+(A⋅B)=AA+(A⋅B)=A
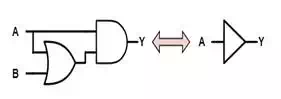
A⋅(A+B)=AA⋅(A+B)=A
Informally, these identities
make sense by considering the possible options. In the first case, if A is
FALSE, then the entire expression is FALSE while if A is TRUE then then (A + B)
is TRUE regardless of the value of B and the expression overall is TRUE. Thus,
in either case, the overall expression is equal to the value of A alone. In the second case this is even more obvious.
If A is TRUE then the overall expression is TRUE while if A is FALSE the second
term is FALSE regardless of the value of B and the overall expression is FALSE.
Again, the overall expression is equal to the value of A alone.
These two identities tend to
be ones that are difficult for people to recall, therefore it is useful to see
an algebraic proof because the manipulations involved are often easier for
people to see and apply than the identities themselves.
In the first identity, we can
either "factor out" the A using the distributive property of AND over
OR or we can just distribute the OR over
the AND. Let's use the first approach as this is the one that is usually easier
to see in practice.
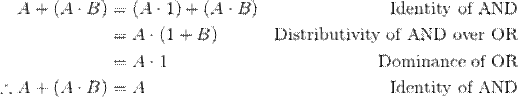
The second identity is
actually more intuitive as see by first distributing the A using the
distributive property of AND over OR and then, after applying idempotence, factoring it back out.
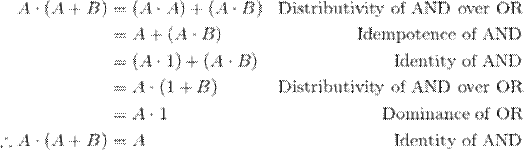
PROOF
|
A |
B |
(A+B)(A+B) |
LHS A⋅(A+B)A⋅(A+B) |
RHS A |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
|
A |
B |
(A⋅B)(A⋅B) |
LHS A+(A⋅B)A+(A⋅B) |
RHS A |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
With the previously proven
identities, the absorption identities can be proven algebraically in very short
order.
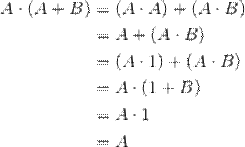
The above prove actually
contains the proof for the absorption identity under AND beginning with the
second line.
DeMorgan's
DeMorgan's identities, better known as DeMorgan's Theorems, are extremely powerful and heavily
used properties of Boolean logic. In essence, they say that and OR gate can be
swapped with an AND gate (and vice-versa) without changing the logic function
being implemented provided that ALL of the inputs and outputs to the gate are
inverted as well.
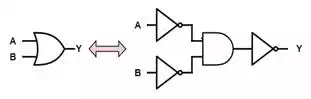
A+B=AŻŻŻŻ⋅BŻŻŻŻŻŻŻŻŻŻŻŻŻŻŻA+B=AŻ⋅BŻŻ
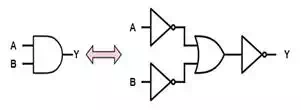
A⋅B=AŻŻŻŻ+BŻŻŻŻŻŻŻŻŻŻŻŻŻŻŻŻŻŻA⋅B=AŻ+BŻŻ
Recalling that a bubble on
either an input or an output of a gate represents logical inversion, DeMorgan's Theorems can be captured very compactly as
follows:

PROOF
|
A |
B |
A + B |
AŻŻŻŻAŻ |
BŻŻŻŻBŻ |
AŻŻŻŻ⋅BŻŻŻŻAŻ⋅BŻ |
LHS A+BA+B |
RHS AŻŻŻŻ⋅BŻŻŻŻŻŻŻŻŻŻŻŻŻŻŻAŻ⋅BŻŻ |
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
|
A |
B |
A⋅BA⋅B |
AŻŻŻŻAŻ |
BŻŻŻŻBŻ |
AŻŻŻŻ+BŻŻŻŻAŻ+BŻ |
LHS A⋅BA⋅B |
RHS AŻŻŻŻ+BŻŻŻŻŻŻŻŻŻŻŻŻŻŻŻŻŻŻAŻ+BŻŻ |
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
Conclusion
Armed with the identities
presented here, you are in a position to manipulate Boolean logic expressions
and logic diagrams. However, these identities are merely the most fundamental
of tools available to you as a logic designer. To become truly proficient at
the art, you must also learn some of the many powerful analysis and design
techniques that are based upon these fundamentals.