An Intro to Power Systems and Reactive Power

Don't know anything about power systems? Here's a start.

The Oldest Field in EE

One of the biggest industries in electrical engineering is power systems. It is the oldest segment of our industry and has been around for over a century, yet not many people know much about its inner workings besides electrical engineers in that field. However, power sytems are something used every day of our lives, so it's important to understand how they work.

Main Components

The power industry is comprised of three main areas: Generation, Transmission, and Distribution. Generation, which happens to be my favorite part, is the actual production of electricity through a number of ways, whether it is through coal and propane or the relatively newer renewable sources such as solar and wind. Most generation is done today through coal and propane, though it is starting to shift towards renewable energy (thankfully).

Transmission is the high voltage power line system (> 135KV normally) that transmits the power from the generation source to the distribution system. The distribution system

converts the very high voltages down to lower, more usable voltages. The distribution system is comprised mostly of 24KV and 12KV lines (varies by state/country) and also includes the substations and transformers. The figure below shows a summary.

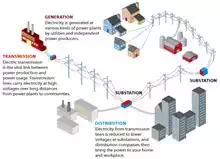
Source: U.S. Department of Energy. "Benefits of Using Mobile Transformers and Mobile Substations for Rapidly Restoring Electric Service: A Report to the United States Congress Pursuant to Section 1816 of the Energy Policy Act of 2005." 2006.

Generation

Generation can be a very tedious task due to electromagnetic fields. It is easy to generate electricity using electrical motors (that’s another topic for another day), but it’s very difficult to do it efficiently (more about this later). The real power is the power generated by all the resistive elements in a power system (P, with unit of Watts), but the other component of power that is not mentioned often is reactive power (Q, with units of VARS). Reactive power is created when AC current and AC Voltage are not in phase.

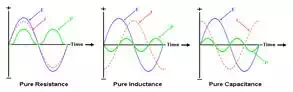
AC voltage and currents can be thought of as sinusoidal wave forms. If you have an AC voltage over a simple resistor, the current will stay in the same phase. If we pass the same voltage over an inductor or capacitor, the current will be out of phase, as these two devices require time to charge and discharge, unlike the resistor, which has no charge or discharge time and only has a voltage drop and power loss.  Specifically, an inductive circuit will cause the current to lag behind the voltage, and a capacitive circuit will cause the current to lead the voltage. A diagram visually explaining this sometimes can be easier to understand (E is the voltage waveform, I is the Current Waveform, and P is power).

Equations

There are several useful and fundamental power equations that engineers and physicists use. One is S=EI, where S is the apparent power (containing the real power in watts and the reactive power in vars. The units for S are volt-amperes where E is the AC voltage waveform and I* is the conjugate of the AC current waveform).

It's strange to think of current and voltage as having an angle, though it does simplify things when you assume the voltage has an angle of 0, since the angles for the current and voltage are in all practical terms relative anyhow. There are two ways to represent AC voltages and currents: rectangular (or complex) form or polar (or phasor) form. This is best explained in an example.

V=IRV=IR

This is the most well-known electrical formula, Ohms law, but here we replace R with Z to account for the fact that most loads are not purely resistive, and have an “imaginary” component to them. Z is known as the impedance.

V=10∠600V=10∠600

Z=5+j5Z=5+j5

Here we have the voltage in phasor form and the impedance in complex format. In electrical engineering, we use j in place of the imaginary i, since i also means current. The conversions between the two are rather simple.

From complex to phasor:

A+jBtoC∠thetaA+jBtoC∠theta

C=A2+B2−−−−−−−√C=A2+B2

θ=tan−1(BA)θ=tan−1(BA)

A=Ccos(θ)A=Ccos(θ)

B=Csin(θ)B=Csin(θ)

From the given V and Z values, the current is calculated to be (phasor form):

I=VZI=VZ

I=1.414∠150I=1.414∠150

Power (Power as a form of Real Watts and Reactive VARs) calculations can be slightly more complex.  The *, as mentioned above, is the conjugate of the current.

S=VI∗=|V|2Z∗=I2ZS=VI∗=|V|2Z∗=I2Z

To obtain the conjugate of the current, you simply negate the angle in phasor form or negate the imaginary coefficient in complex format. So the complex power here would be 14.14 < 75°.  Complex power can also be represented in complex form as P+jQ-- as we’ve mentioned before, P is the real power and Q is the reactive power.  So applying the same conversion from complex to phasor and vice versa, we can easily obtain the following formulas

P=VIcos(θ)P=VIcos(θ)

Q=VIsin(θ)Q=VIsin(θ)

P is the real power that consumers pay for, but why is reactive power such an important thing in the power industry?

Like most businesses, the answer is cost. Simply put, when there is a net reactive power loss in a system, it costs power plants more resources to output that power. Mathematically put, when Q is not 0 (power factor is lagging or positive, can be positive or negative), the magnitude of I is higher than if would be if Q is zero (power factor is unity). Having to generate a higher

current magnitude can be very costly to a power plant.

In the end, power plants and generating facilities are always trying to cancel out whatever net value of Q is on the system. For most systems, the net Q on the systems tends to be  positive (lagging); this is because most loads on the system will tend to be inductive due to motor loads think air-conditioning units and transformers, which are always present on every system regardless of residential, commercial or industrial use.  To offset this mostly inductive load, utilities will install large switching capacitor banks on a distribution and transmission system to help balance out. These banks will switch on and off depending on their need at the time, usually they are switched on during peak load usage times.

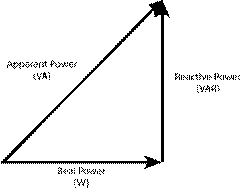
There is not a perfect system out there, as it is cost prohibitive. But generally power factor for a system is kept above .95 for most areas. Visually, power plants are trying to bring this power triangle to unity (a straight line).

There are many specializations in the power industry; this article only scratches the surface. The technology is constantly changing and forcing engineers to think of new ways to come up with solutions to the problems and challenges that it may bring. In my opinion, the main challenges we face today are the effects of climate change and what role the power industry plays in it, as well as emerging and newly developed countries and their appetite for electric power. In this area, only one thing is certain: there will always be a need for power engineers.