Understanding Inductor Designs for Converters

A demonstration of filter inductor design for boost converters, design of the coupled inductor for a two-output forward converter, and the design of flyback transformer in continuous conduction mode.

The filter inductor in the converter circuit is operated in a small B-H loop region as compared to the wide region for the conventional transformer. The area of B-H loop is proportional to the total current ripple in the inductor. The core losses are negligible, according to the minor B-H loop area. On the other hand, copper loss depends on the DC current flowing through inductor. The same curve is also applicable in the case of coupled inductor. Design is majorly constrained by the copper loss and the saturation condition of the filter inductor.

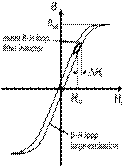
Figure 1. B-H Loop for Filter Inductor 

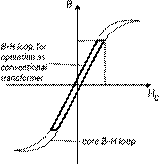
Figure 2. B-H loop for the Conventional Transformer

Design of an Inductor for Boost Converter

The circuit diagram of the boost converter with related waveform under CCM:

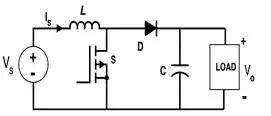
Figure 3. Circuit of Boost Converter

The basic constraints for the design of an inductor are (a) keep the flux density B below the flux density at the saturation BSAT (b) keep the temperature of the inductor within limit. We also want the inductor current ripples to be equal to the ∈ part of the inductor current.(Ripples in the Inductor << Inductor Current)

We should know the requirements for this converter circuit according to the following given specifications:

            VS, VO, f, PO

Where,

            VS = Input Voltage

            VO = Output Voltage

            f = Operating frequency in kHz. (f=1T)

            PO = Output power in kW

We can get the duty ratio of the boost converter by this equation:

D=VO−VSVOD=VO−VSVO

The input DC current of the converter is the inductor current which is given by this equation:

IL=IS=IO1−D=POVO1−DIL=IS=IO1−D=POVO1−D

We have seen earlier that,

Imin=DVSR(1−D)2−VS2LDT=Iavg−∆ILImin=DVSR(1−D)2−VS2LDT=Iavg−∆IL

Imax=DVSR(1−D)2+VS2LDT=Iavg+∆ILImax=DVSR(1−D)2+VS2LDT=Iavg+∆IL

Thus,

∆IL=VS2LDT∆IL=VS2LDT

  [Equation 1]

Also,

∆IL=∈IL∆IL=∈IL

 [Equation 2]

Thus, the required inductance value from Equations 1 and 2 is given by

L=VSDT2∈ILL=VSDT2∈IL

R.M.S value of the inductor current in the case of a triangular wave is given by the following expression:

(ILrms)2=(Iavg)2+112(Ipp)2=(Iin)2+112(∆I)2(ILrms)2=(Iavg)2+112(Ipp)2=(Iin)2+112(∆I)2

⇒ILrms=(ILdc)2+112(2∆IL)2−−−−−−−−−−−−−−−−−√⇒ILrms=(ILdc)2+112(2∆IL)2

R.M.S value of voltage across inductor is given by

VLrms=DVS2+(1−D)(VO−VS)2−−−−−−−−−−−−−−−−−−−−−√VLrms=DVS2+(1−D)(VO−VS)2

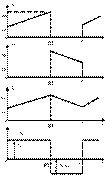
Figure 4. Supply Current, Diode Current, Inductor Current and Inductor Voltage respectively (Boost Converter)

If the frequency of the converter is not less than the apparent frequency obtained from the following expressions, it is a worst-case frequency.

fapparent=VLrms2πLfapparent=VLrms2πL

is valid for the low-frequency range under low eddy current losses and d<1.6δ. Consider the fill factor FC according to the type of conductor (round wire or litz wire). Now, we have all the input parameters in designing an inductor. We can determine the core parameters AC', AW, and lmeanT using the constraint equations below.

NIm≈BmAC′Rg=BmAC′lgμONIm≈BmAC′Rg=BmAC′lgμO

Rw=ρlwrAC=ρNlmeanTACRw=ρlwrAC=ρNlmeanTAC

L=N2Rg=µOAC′N2lgL=N2Rg=µOAC′N2lg

FCAW≈NACFCAW≈NAC

We will then get the required final volume of the core. We can now also multiply the volume with the corresponding power density of the material at a particular frequency to measure core loss. Power density is measured by the plot between the power density at a particular frequency and the change in the magnetic flux density given by the manufacturer. Change in flux density is given by:

∆B=VLN1AC′(DT)∆B=VLN1AC′(DT)

We can neglect the core loss if it is comparatively less than the copper loss, and use the material which has higher core loss and high saturation flux density. This leads to a smaller size inductor core.

Design of a Coupled Inductor for a Two-Output Forward Converter

Coupled inductors have multiple windings wound on the same core for high value of inductance in common mode current while low value of inductance for the differential mode current. Coupled inductors have lower leakage inductance and AC current losses. Consider a coupled inductor as shown in the figure below:

Figure 5. Coupled Inductor

The number of turns for L1and L2 must be same to maintain the volt-time balance condition. Magnetizing field is produced by the sum of the currents i.e. i1+i2 which flows through the core. Leakage field is produced by the difference of the currents i.e. i1-i2 which flows through air.  The circuit diagram for the two-output forward converter using coupled inductor is given below.

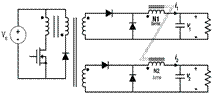
Figure 6. Circuit for the Two-Output Forward Converter

Common Mode Current, 

ic=i1+i22ic=i1+i22

Differential Mode Current,

id=i1−i22id=i1−i22

These currents both contribute in the eddy current losses.

Common Mode Inductance,

Lc=N2Rm=PmN2Lc=N2Rm=PmN2

Differential Mode Inductance,

Ld=N2RO=PON2Ld=N2RO=PON2

Here, Pis the permeance provided by the manufacturer and R is the reluctance. For common mode current, coupled inductors act like two inductors L1and L2 in parallel. For differential mode, coupled inductors act like a transformer. There is a considerable DC component in the current flowing through L1and L2 which causes the net magnetization of the core.

H(t)=N1i1(t)+N2i2(t)lCRmRm+ROH(t)=N1i1(t)+N2i2(t)lCRmRm+RO

Similar design procedure with the single-winding filter inductor is used.

Design of a Flyback Transformer in CCM

The flyback transformer acts as an inductor, having two windings where only one of its windings carries the current at a particular time. The flyback transformer stores the energy and releases it later, which requires an air gap. As both the windings carry the current alternatively even with the continuous total ampere-turns, high AC winding losses are associated with the flyback converter irrespective of its operating mode.  Core loss depends on the magnetizing current Im for the transformer and is usually significant in the case of the discontinuous conduction mode.

In CCM, conversion ratio for the converter is:

VOVS=D1−D.VOVS=D1−D.

For the desired duty cycle and nominal supply voltage, the initially expected turns ratio is given by:

n=vsvo′D1−D=N1N2n=vsvo′D1−D=N1N2

where  vo' is the sum of the voltages across the load, switch, rectifier and copper loss referred to the secondary side. We even need to see the duty ratio for the worst-case current of the DC and AC components. Duty cycle and turns ratio can be possibly altered to optimize the design. We can select the particular material according to the proper specifications with the help of the data sheet.

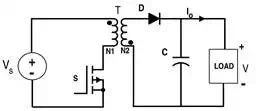
Figure 7. Circuit for Flyback Converter

Core loss is negligible and flux density is restricted by the saturation of the core. Net field in the core is the sum of the magnetizing current and the leakage field. Magnetizing field is used for the storage of energy and basically acts as an inductor while the leakage field performs like a transformer.

Bn(t)=Bm(t)+Bl(t)Bn(t)=Bm(t)+Bl(t)

Change in Magnetic flux density can obtained by

∆Bm=Bm∆ImIsc∆Bm=Bm∆ImIsc

Here, Isc is the short-circuit current which produces the maximum flux density.

The number of turns on the secondary side is given by

Ns=L∆Im∆BmAcNs=L∆Im∆BmAc

Thus, the corresponding turns for the secondary can be calculated. Select the core shape and its type using the guide provided by the manufacturer. Based on that, we need to calculate the thermal resistance, conductor size, air gap length, winding loss, DC and AC losses consequently.

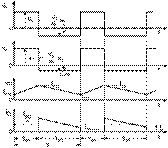
Figure 8. Waveforms of Input Voltage, Output Voltage, Magnetizing Current, and Diode Current for the Flyback Converter