Discontinuous Conduction Mode of Simple Converters

Discussed here are the discontinuous conduction mode, mode boundary, and conversion ratio of simple converters.

Origin of the Discontinuous Conduction Mode

During continuous conduction mode, the inductor current in the energy transfer never reaches zero value. In the case of the discontinuous conduction mode, the inductor current falls to zero level which is very common in DC-to-DC converters.

If the peak of the inductor current ripples is less than the DC component of the inductor current, the diode current is always positive and the diode is forced to turn on when the switch S (either a transistor or thyristor) is off. On the other hand, if the peak of the inductor current ripples becomes more than the DC component of the inductor current, the total current falls to zero value while the diode is conducting. Thus, the diode will stop conducting and the inductor current will remain at zero value until the switch S will be gated again due to the polarity reversal across the switch. This gives rise to the discontinuous conduction mode in the chopper or the DC-to-DC converter.

In the discontinuous conduction mode, inductor current is not persistent throughout the complete cycle and reaches zero level earlier even before the end of the period. Discontinuous conduction mode inductance is less than the minimum value of the inductance for the continuous conduction mode,

                LDCM < LCCM.

Thus, this condition generally arises for the light-load condition.

Let the value of inductance in the case of the discontinuous conduction mode be,

                 LDCM=ξ LCCM where  0<ξ<1 for the discontinuous conduction.

The discontinuous conduction mode usually occurs in converters which consist of single-quadrant switches and may also occur in converters with two-quadrant switches. Two-level DC buck, and boost and buck-boost converters will be discussed further in this article. There are two levels indicated here towards the two-voltage level for the inductor voltage.

The energy stored in the inductor is proportional to the square of the current flowing through it. Having the same power through the converter, the requirement of the inductor current is higher in the case of the discontinuous conduction as compared to the continuous conduction mode. This causes more losses in the circuit of the discontinuous conduction. As the energy stored is not yet released to the output in the discontinuous conduction, the output gets affected by the ringing. This may also cause a noise in the discontinuous conduction mode.

Moreover, the value of the inductance required for discontinuous conduction mode is lesser as compared to the continuous conduction mode since it  allows the fall of the inductor current to zero level. This causes higher values for the root-mean-square and the peak current. Thus, the size of the  transformer required in isolated converters is bigger as compared to the  continuous-conduction transformer size to suit the larger flux linkage and the losses.

Conversion ratio is independent of the load during the continuous conduction mode but when it enters in discontinuous conduction mode, it becomes dependent to the load. This complicates the DC-circuit analysis because the first-order equations become second order.

In most of the applications, continuous conduction mode is employed. Yet, discontinuous conduction mode can also be used for certain applications such as for the low-current and loop-compensation applications.

Buck Converter

Consider the simple buck converter circuit shown in Fig. 1. The current in the converter is controlled here by two switches labeled as S (MOSFET) and D (Diode).

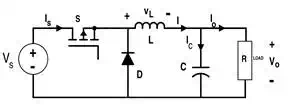
Figure 1. Circuit for Buck Converter

This is a single-quadrant converter with the following waveforms for the continuous conduction mode shown in Fig. 2.

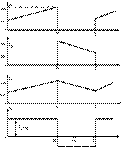
Figure 2. Supply Current IS, Diode Current ID, Inductor Current I, and Inductor Voltage VL Waveforms respectively (Buck Converter)

The buck converter in discontinuous and continuous conduction modes are in the second-order and first-order systems respectively.

For continuous conduction mode,

IL+=1L∫t0(VS−VO)dt+IminIL+=1L∫0t(VS−VO)dt+Imin

  For 0≤t≤DT.

⇒IL+=VS−VOLt+Imin⇒IL+=VS−VOLt+Imin

At t=DT, inductor current is at maximum value,

Imax=VS−VOLDT+IminImax=VS−VOLDT+Imin

    [Equation 1]

IL−=(1L)∫tDT−VOdt+ImaxIL−=(1L)∫DTt−VOdt+Imax

   For DT≤t≤T.

⇒IL−=VOL(DT−t)+Imin⇒IL−=VOL(DT−t)+Imin

The average value of the inductor current for the buck converter is

Iavg=VOR.Iavg=VOR.

Because the inductor is always connected to the load whether the switch is on or off.

The average value of the current through the capacitor is nil due to the capacitor charge balance condition.

From Fig. 2, the area under the inductor current waveform is,

(Area)L=TImin+12T(Imax−Imin)(Area)L=TImin+12T(Imax−Imin)

Average value of the inductor current is,

Iavg=VOR=Imin+12(Imax−Imin)Iavg=VOR=Imin+12(Imax−Imin)

    [Equation 2]

From Equations 1 and 2 we can get,

Iavg=VS−VO2LDT+IminIavg=VS−VO2LDT+Imin

⇒Iavg=D(VS−VO)2Lf+Imin=VOR⇒Iavg=D(VS−VO)2Lf+Imin=VOR

The value of inductance is,

L=D(VS−VO)R2f(VO−IminR)L=D(VS−VO)R2f(VO−IminR)

The boundary of continuous condition is when Imin=0. If the value of Imin<0, the converter enters in the discontinuous conduction mode.

Thus,

             L=LCCM for Imin=0

Hence,

LCCM=D(VS−VO)R2fVOLCCM=D(VS−VO)R2fVO

The value of inductance for the discontinuous conduction is given by

L=LDCM=ξLCCM=ξD(VS−VO)R2fVO,L=LDCM=ξLCCM=ξD(VS−VO)R2fVO,

where 0<ξ<1.

For discontinuous conduction mode, when L< LCCM, the waveforms for the inductor current and inductor voltage are shown in Fig.3.

Figure 3. Inductor Current and Voltage for the Discontinuous Conduction Mode of Buck Converter

It is clear from the Fig.3 that the value of the minimum inductor current is zero i.e. Imin=0.

As the current across the inductor current is reduced to zero, the value of the voltage across the inductor is also reduced to zero value while VC =VO during the entire cycle.

For the time duration 0 ≤ t ≤ TON

IL+(t)=VS−VOLtIL+(t)=VS−VOLt

     [Equation 3]

As the value of the peak inductor current occurs at t = TON,

⇒Imax=VS−VOLTON=VS−VOLDT=VS−VOLfD.⇒Imax=VS−VOLTON=VS−VOLDT=VS−VOLfD.

For the time duration      TON ≤ t ≤ TX,

IL−(t)=∫tTON−VCLdt+ImaxIL−(t)=∫TONt−VCLdt+Imax

⇒IL−(t)=VCL(TON−t)+VS−VOLf⇒IL−(t)=VCL(TON−t)+VS−VOLf

   [Equation 4]

At t = TX, current reduces to zero value,

0=VCL(TON−TX)+VS−VOLf0=VCL(TON−TX)+VS−VOLf

⇒TX=DVSfVO⇒TX=DVSfVO

Compared to the continuous condition, the amount of energy needed by the load is lesser in the discontinuous condition.

It is considered that the converter is operated in the steady state. Thus, the energy in the inductor remains the same at the start and at the end of the cycle. The volt-time balance condition can also be applied here.

The above equation can also be derived using the inductor volt-second balance condition as,

(VS−VC)TON+(−VC)(TX−TON)=0(VS−VC)TON+(−VC)(TX−TON)=0

⇒(VS−VC)DT+(−VC)(TX−DT)=0⇒(VS−VC)DT+(−VC)(TX−DT)=0

⇒TX=VSDfVO⇒TX=VSDfVO

For the time duration     TX ≤ t ≤ T

IL0(t)=0IL0(t)=0

From the Fig. 3, it is clear that the average value of the inductor current is equal to the area under the load current curve divided by T.

Iavg=12TXImaxTIavg=12TXImaxT

For the DC supply,

Iavg=VORIavg=VOR

Hence,

VOR=VS(VS−VO)D22LVOfVOR=VS(VS−VO)D22LVOf

The duty cycle ratio for the discontinuous conduction mode in the case of the buck converter is,

D=VO2LfRVS(VS−VO)−−−−−−−−−−−−√D=VO2LfRVS(VS−VO)

    [Equation 5]

The duty cycle ratio of the buck converter in its continuous conduction mode is

D=VOVi.D=VOVi.

The duty cycle ratio for the buck converter is also dependent on the inductance L, load resistance R, and the switching frequency f.

For discontinuous conduction mode,

L=LDCM=ξLCCM=ξD(VS−VO)R2fVOL=LDCM=ξLCCM=ξD(VS−VO)R2fVO

   [Equation 6]

Substitution of the Equation 5 into Equation 6 gives,

D=VOVSξ√D=VOVSξ

    [Equation 7]

Since 0 < ξ < 1, duty cycle ratio of the buck converter in the discontinuous conduction mode is less than its value in the continuous conduction mode. Thus, less amount of energy is transferred through the converter which is not enough to maintain the inductor current throughout the entire period. This is the reason the discontinuous current flows through the inductor.

The conversion ratio of buck DC-to-DC converter is,

VOVS=Dξ√VOVS=Dξ

where 0<ξ<1

If the value of ξ is greater than 1, the converter enters in the continuous conduction mode. We can easily know the conduction state of the buck converter, which is either continuous or discontinuous, if we know the value of input and output voltages of the converter by simply measuring the value of ξ.

Instantaneous value of the capacitor current is given by subtracting the value of the inductor current to the load current. When the inductor current value is reduced to zero value, the load current is supplied by the capacitor.

From Equations 3 and 4 we can get:

For the time duration 0 < t

IC+(t)=VS−VOLt−IOIC+(t)=VS−VOLt−IO

   [Equation 8]

For the time duration DT < t < TX,

IC−(t)=VOL(DT−t)+D(VS−VO)Lf−IOIC−(t)=VOL(DT−t)+D(VS−VO)Lf−IO

    [Equation 9]

And for the time duration TX < t < T,

ICO=−IOICO=−IO

    [Equation 10]

If the capacitance is assumed to be ideal, the capacitor current will not decay even after the inductor current value is reduced to zero value. For that case, the waveforms for the capacitor and inductor current are shown in Fig. 4.

From Fig.4, it is clear that the value of the capacitor current is zero at time t=Ta and at t=Tb.

Equation 8 at time t =Ta gives,

0=VS−VOLTa−IO0=VS−VOLTa−IO

⇒Ta=LIOVS−VO⇒Ta=LIOVS−VO

   [Equation 11]

And Equation 9 at time t=Tb gives,

0=VO(DT−Tb)L+D(VS−VO)Lf−IO0=VO(DT−Tb)L+D(VS−VO)Lf−IO

⇒Tb=DT−LIOVO+D(VS−VO)fVO⇒Tb=DT−LIOVO+D(VS−VO)fVO

   [Equation 12]

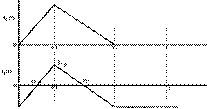
Figure 4. Inductor Current and Capacitor Current respectively for the Discontinuous Conduction Mode

of the Buck Converter

The positive time interval for the charge accumulation i.e. Tb-Ta from Equations  11 and 12 is given by:

Tb−Ta=DVSfVO−LIOVSVO(VS−VO)Tb−Ta=DVSfVO−LIOVSVO(VS−VO)

    [Equation 13]

From Equation 6 and Equation 7 we can get,

Tb−Ta=2ξ√−ξ2fTb−Ta=2ξ−ξ2f

    [Equation 14]

From Fig.4, it is also clear that the maximum value of the capacitor current occurs at the time t=DT.

At t = DT,

IC(DT) = Ihp

From Equation 8 we can get,

Ihp=(2ξ√−1)IOIhp=(2ξ−1)IO

    [Equation 15]

The charge accumulated is the integration of the capacitor current (area under the capacitor current from Ta  to Tb) which is also given by the expression:

          ∆Q=C∆V   [Equation 16]

Thus,

C∆V=12(2ξ√−ξ)(2ξ√−1)IO(12f)=VO(2−ξ√)24RfC∆V=12(2ξ−ξ)(2ξ−1)IO(12f)=VO(2−ξ)24Rf

The ripples in the load due to the ripples in the capacitor are given by the following expression:

r=∆VVO=(2−ξ√)24Rfr=∆VVO=(2−ξ)24Rf

Boost Converter

Circuit for the boost converter is shown in Fig. 5.

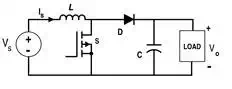
Figure 5. Circuit for Boost Converter

The waveform for the continuous conduction mode is shown in Fig. 6. When it is in the discontinuous conduction mode, the waveform is shown in Fig. 7.

We can assume that the inductor is connected to the load for the time Ty such that

                   IO =Y Iavg    [Equation 17]

where

                     Y = Ty/T

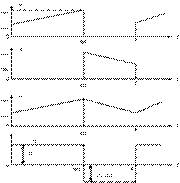
Figure 6. Supply Current, Diode Current, Inductor Current and Inductor Voltage respectively (Boost Converter)

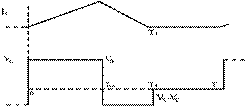
Figure 7. Inductor Current and Voltage for the Discontinuous Conduction Mode of Boost Converter

When the converter operates in the steady-state condition, the energy at the start and at the end of the cycle is the same. Thus, volt-time balance condition can be applied here too.

From the figure and the volt-time balance condition it is clear that,

          TON VS+(TX-TON).(VS-VC)=0

⇒DTVS+(TX−DT).(VS−VO)=0⇒DTVS+(TX−DT).(VS−VO)=0

⇒TX=DVO(VS−VO)f⇒TX=DVO(VS−VO)f

From Fig. 6, it is also evident that the value of the minimum and maximum currents are as follows:

Imin=0;

and

Imax=VSLTON=VSLfDImax=VSLTON=VSLfD

Thus, the average value of the inductor current is,

Iavg=11−DVOR=12TXImaxTIavg=11−DVOR=12TXImaxT

⇒VOR=(12)(DVO(VS−VO)f)(VSDLf)(1−D)T⇒VOR=(12)(DVO(VS−VO)f)(VSDLf)(1−D)T

From Equation 17 we can get,

D=2(VO−VS)LfRYVS−−−−−−−−−−−−√D=2(VO−VS)LfRYVS

    [Equation 18]

The duty cycle ratio of the buck converter for the continuous conduction mode is equal to

VO−VSVS.VO−VSVS.

In the discontinuous conduction mode, the duty cycle ratio of the boost converter is not only dependent on the input and output voltages but it also depends on the inductance L, load resistance R, and the switching frequency f.

The discontinuous inductance for the boost converter is,

LDCM=ξYRVS(VO−VS)2fVOLDCM=ξYRVS(VO−VS)2fVO

Substituting this value of inductance in Equation 18 we can  get,

D=VO−VSVOξ√D=VO−VSVOξ

⇒VOVS=VS1−Dξ√⇒VOVS=VS1−Dξ

Hence, the complete conversion ratio for the boost converter in the discontinuous conduction mode is given by the above expression.

Buck-Boost Converter

The circuit for the buck-boost converter is shown in Fig. 8 and the related waveforms of the buck-boost converter in the case of continuous conduction mode are shown in Fig. 9.

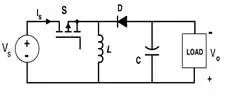
Figure 8. Circuit for the Buck-Boost Converter

Inductor is connected to the load during the switch-off period; where Y= (1-D).

Thus,

Iavg=YIO=YVOR=(1−D)VORIavg=YIO=YVOR=(1−D)VOR

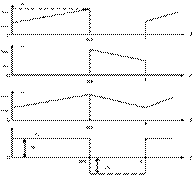
Figure 9. Supply Current, Diode Current, Inductor Current and Inductor Voltage respectively (Buck-Boost Converter) in Continuous Conduction Mode

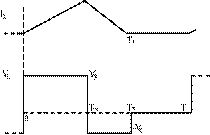
Figure 10. Inductor Current and Inductor Voltage for the Discontinuous Conduction Mode

of the Buck-Boost Converter

Assume that the converter is operating in steady state; therefore, energy at the start up to the end of the cycle must be equal. Thus, volt-time balance condition is applied here.

Applying the volt-sec balance across the inductor using the Fig. 9,

           VS TON + (TX - TON) (-VO) = 0

⇒VSDT−(TX−DT)VO=0⇒VSDT−(TX−DT)VO=0

⇒TX=D(VS+VO)VOf⇒TX=D(VS+VO)VOf

From the Fig. 9, it is also noticed that the value of the minimum and maximum currents are as follows:

Imin = 0

Imax=VSLTON=VSLfDImax=VSLTON=VSLfD

Thus, the average value of the inductor current  is,

Iavg=YVOR=12ImaxTXTIavg=YVOR=12ImaxTXT

⇒VOR=12VSDLfD(VS+VO)YVOff⇒VOR=12VSDLfD(VS+VO)YVOff

In the discontinuous conduction mode of the buck-boost converter, the value of the duty cycle ratio is given by

D=VO2LfRYVS(VS+VO)−−−−−−−−−−−−−√D=VO2LfRYVS(VS+VO)

The duty cycle ratio of the buck-boost converter for the continuous conduction mode is equal to

VOVO+VS.VOVO+VS.

In the case of the discontinuous conduction mode, the duty cycle ratio of the buck-boost converter is also dependent on the inductance L, load resistance R, and the switching frequency f.

The conversion ratio for the buck-boost converter is,

VOVS=Dξ√−D