Understanding Analog-to-Digital Converters: Deciphering Resolution and Sampling Rate

Perhaps two of the most important characteristics to consider during the selection process for analog-to-digital converters (ADCs) are the resolution and the sampling rate. Before any selection can take place these two factors should be considered carefully. They will affect everything in the selection process from price to the underlying architecture of the analog-to-digital converter required. In order to properly determine the correct resolution and the correct sampling rate for a specific application, a reasonable understanding of these characteristics should be obtained.

What follows here are some mathematical descriptions of the terms associated with analog-to-digital conversion. The mathematics is important, but the concepts that it represents are even more important. If you can bear through the mathematics and understand the concepts introduced, you will be able to narrow down the number of appropriate ADCs for your application and selection will become that much easier.

Quantisation

An analog-to-digital converter converts a continuous signal, either a voltage or a current, into a sequence of numbers represented by discrete logic levels. The term quantisation refers to the process of converting a large set of values to a smaller set, or discrete set, of values. Mathematically, an ADC can be described as quantising a function with a large domain to produce a function with a smaller domain.

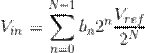
$Title: V_{in}=\sum_{n=0}^{N-1}b_n2^n\frac{V_{ref}}{2^N}$

The equation above describes the analog-to-digital conversion process mathematically. Here we are describing the input voltage Vin as a series of bits bN-1...b0. In this formula 2N represents the number of quantisation levels. It is intuitive that more quantisation levels result in a more precise digital representation of the original analog signal. For example, if we can represent the signal with 1024 quantisation levels instead of 256 levels, we have increased the precision of the ADC because each quantisation level represents a smaller amplitude range.

Vref represents the maximum input voltage that can be successfully converted to an accurate digital representation. As such, it is important that Vref be larger, or the same as, the maximum value of Vin. Bear in mind, however, that a value much larger than the value of Vin will result in fewer quantisation levels representing the original signal. For example, if we know our signal will never increase above 2.4 V, it would be inefficient to use a voltage reference of 5 V because over half of the quantisation levels would be unused.

Quantisation Error

Quantisation error is a term used to describe the difference between the original signal and the discrete representation of the signal.

$Title: q= \frac{2A}{2^N}$

One quantum can be described as shown above in which A represents the amplitude and the signal spans from A to -A. N represents the number of bits the signal is quantised to.

Now that we have investigated quantisation, it is time to see what quantisation means for an ADC. In order to do this, we need to do some more mathematics. The equation below describes quantisation error.

$Title: \epsilon= \frac{\pm{q}}{2}=\pm{A}.2^{-N}$

From this, the power in quantisation error can be defined as shown below.

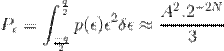
$Title: P_{\epsilon}= \int_{\frac{-q}{2}}^{\frac{q}{2}}p(\epsilon) \epsilon^2\delta\epsilon \approx \frac{A^2.2^{-2N}}{3}$

Consider the signal in the figure above. The power of the signal can be defined as shown in the equation below.

$Title: P_{s}= \frac{A^2}{T}\int_{0}^{T}sin^2\omega t \delta t = \frac{A^2}{2}$

Thus, the signal to quantisation noise ratio (SQNR) can be defined in decibels as shown below. From this equation it becomes obvious that an ADC with a larger number of quantisation levels results in an improved SQNR ratio.

$Title: 10log_{10}\frac{P_s}{P_\epsilon}=1.76+6.02N (dB)$

The SQNR value would be the signal to noise ration (SNR) for an ideal ADC. Unfortunately, there are other sources of noise associated with the analog-to-digital conversion process. Nevertheless, determining the SQNR required for your application, by careful analysis and consideration of the analog signal, will aid in the selection process. The number of quantisation bits of a given analog to digital converter is know as its resolution.

Characteristic 1: Resolution - The number of quantisation bits of an ADC.

In most applications, it is preferable to get the maximum resolution possible. This resolution is often limited by other considerations such as resources in the digital domain and cost. As a result, it is important to determine the minimum resolution required for your application.

Sampling

The continuous time domain signal not only needs to be quantised in terms of amplitude, it also needs to be quantised in terms of time. Consider a train of impulses described as below, where the term Ts can be defined as the sampling time period.

$Title: w(t)=\delta(t-nT_s)$

The sampled signal y(t) can be defined mathematically as shown in the equation below.

For the impulse train and analog signal in the figure above, this results in the impulse train as seen in the figure below.

The Dirac delta function is helpful in describing the concept of sampling mathematically and will come in useful when looking at signals in the frequency domain. It is worth mentioning, however, that in real life electronics, these functions do not exist. Instead, these are replaced with pulses that are close to rectangular.

The Nyquist Criterion and Shannon’s Theorem

In order to determine the sampling rate required, it is necessary to take a look at the frequency domain of the analog signal. This requires again a few mathematical prerequisites. The Fourier transform of w(t) can be defined as shown in the equation below.

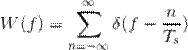
$Title: W(f)=\sum_{n=-\infty}^{\infty}\delta(f-\frac{n}{T_s})$

This equation essentially means that we get a repetition of the Dirac delta function at every harmonic of its frequency Fs. Now lets consider an analog signal with the frequency spectrum as shown in the figure below. The spectrum of the sampled signal Y(f) it turns out will actually be the convolution of X(f) with W(f).

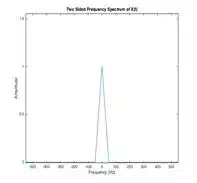
$Title: Y(f)=\int_{-\infty}^{\infty}X(\Theta) W(f-\Theta)\delta\Theta$

This means that, after sampling, the signal repeats for all multiples of the sampling frequency. As shown in the figure below, if the sampling frequency is insufficiently large, the spectral images of the signal overlap. This minimum frequency is defined as twice the bandwidth of the signal to be sampled and is know as the Nyquist Rate.

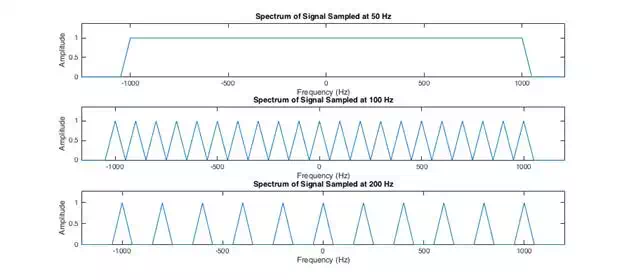
As a result of the Nyquist criterion, it becomes clear that in order to properly specify the correct ADC for an application, we must know the spectral content of the analog signal.

One way to ensure the Nyquist criterion is met is to filter the analog signal prior to digitizing. This is known as an anti-aliasing filter. If we know the frequency band of interest, we can filter the analog signal with an anti-aliasing filter to ensure that no frequencies outside of this range are present before digtizing the signal with an ADC.

If we look at the figure above once more, it can easily be seen that after filtering with an appropriate filter, the spectrum is exactly the same as that of the original signal. No information is lost and the original signal can be reconstructed. This is known as Shannon’s Theorem.

Characteristic 2: Sampling Rate - The frequency at which the analog signal is sampled.

Both ADC sampling rate and resolution need to be considered carefully when specifying the ADC required for an application. Often, a compromise needs to be struck between sampling rate and resolution in order to accurately and precisely digitize an analog signal. Before specifying an ADC, it is important to know what sampling rate and what resolution are required. Careful analysis of the analog signal and the digital resources required to process the digital data needs to be performed in order to properly specify the resolution and sampling rate required. This is a very small part of the complete picture, but provides an introduction to some of the key concepts associated with analog-to-digital converters. With a better understanding of quantisation and sampling theorem, we can ease the selection process to a certain extent by systematically determining the best ADC for the job.

From here it is necessary to look at specific ADC architectures in order to determine the best ADC for the job. This includes:

● Successive Approximation Register ADCs

● Delta-Sigma ADCs

● Flash ADCs