Learning About Differential Quadrature Phase Shift Keying (DQPSK) Modulation

This technical brief explains what differential QPSK is and why it can be advantageous compared to ordinary QPSK.

Supporting Information

If you are not familiar with QPSK modulation, you should start with this article.

In theory, QPSK is an excellent RF communication scheme. It is conceptually straightforward, it transfers two bits per symbol instead of one, and it can be conveniently implemented using I/Q modulation techniques.

As usual, though, real life is not quite as neat and tidy as the theoretical version. The particular problem we’re concerned with here is an additional and unpredictable phase shift introduced by a lack of phase or frequency synchronization between the transmitter hardware and the receiver hardware.

The QPSK transmitter has a local oscillator that generates the sinusoid used as the carrier wave. The receiver has a local oscillator that generates a sinusoid used in demodulating the incoming signal. Ideally, these two oscillators have exactly the same phase and frequency.

In reality, of course, there will be discrepancies. The frequencies can be matched quite well thanks to high-precision oscillation devices, but synchronizing the phase is not so easy. A phase or frequency offset between the received signal and the receiver’s local oscillator will introduce error into the phase of the received signals, and this error could cause the receiver to assign an incorrect two-bit code to a particular symbol.

It is possible to design a receiver that can extract the phase and frequency of the incoming carrier. This process is known as carrier recovery, and it can be used to achieve coherent (i.e., phase-and-frequency-synchronized) demodulation. The trouble is, coherent receivers are more complicated and more expensive. Many systems would benefit from a modulation scheme that avoids the error associated with phase or frequency offset yet does not require the additional cost and complexity of carrier recovery.

This is where differential quadrature phase shift keying (DQPSK) comes into play.

In QPSK, information is conveyed by the absolute phase of each symbol. DQPSK, in contrast, conveys information by establishing a certain phase of one symbol relative to the previous symbol. The following diagram illustrates this distinction.

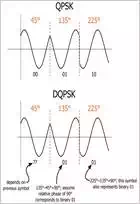
The relative phase is simply the phase of the current symbol minus the phase of the previous symbol. If we use the standard four QPSK phase values—45°, 135°, 225°, and 315°—the DQPSK phase options become 0°, 90°, –90°, and 180° (or, equivalently, –180°).

By using relative phase instead of absolute phase, DQPSK is not affected by a fixed phase offset introduced by lack of phase synchronization between transmitter and receiver; the fixed offset affects both symbols equally and is eliminated in the subtraction process. DQPSK is also robust against transmitter–receiver frequency discrepancies.

Even though a frequency offset introduces a time-varying phase error, as long as this error changes slowly relative to the symbol rate, the differential phase from one symbol to the next will remain accurate enough for reliable data transfer.

Compared to carrier recovery, this differential phase detection process does not constitute a major increase in the complexity of the receiver; this is especially true if the conversion from analog baseband to digital data is performed in software.

One disadvantage to keep in mind, though, is the effect of noise: theoretically, a coherent QPSK system would have a lower bit error rate because the received symbol is compared to an ideal reference signal, whereas in DQPSK a noisy symbol is compared to another noisy symbol.