Everything You Need to
Know About Direct Digital Synthesis
Introduction
Direct digital synthesis
(DDS) is a technique used to generate an analog signal
(like a sine wave or triangle wave) using digital techniques. The analog signals are synthesized from values stored in
memory. A "template" containing the signal's amplitude values for all
waveform phases is stored in memory and used to recreate the signal. With DDS,
signals can be synthesized directly from the template without requiring the
phase-locked loops other indirect methods require. Different frequencies are
produced by changing the rate the phase values are processed and using
techniques to add, multiply and scale signals, various waveforms can be
generated. The synthesized signals are repeatable and the frequencies precise.
Communication techniques like spread spectrum frequency hopping use DDS to
quickly change frequencies. It is also used for signal generators and enables
frequency sweeps.
Benefits
To understand the benefits of
DDS, consider the situation with radio receivers. If using an analog tuned radio when trying to tune to a specific
station, you adjust whatever knobs, thumb-wheels, and sliders are provided. You
may hit the station exactly one time... but then it may take a while to tune it
in another time. And just because you tuned it once, doesn't mean there isn't
drifting, forcing you to re-tune. When you have a digital tuner, you enter the
station you want and the electronics lock it in.
In the same way, using analog components to generate signals means
adjustments and time to get the frequency correct, without any guarantee the
output will be consistent. DDS with conditioning circuits allow a specific
frequency to be set quickly, consistently, and repeatedly.
DDS has had a big impact in
testing. Before DDS frequency generators, trying to produce accurate frequency
response plots was a frustrating effort. When testing extremely narrow band,
high-order, high-Q filters, when assessing filter
performance over a temperature range, accurate and repeatable frequencies are
required at resolutions that analog generators
can't provide. Some radio frequency (RF) modulation techniques depend on
accurate frequency generation only possible with DDS. When scanning radio frequencies
for signals and power measurements, DDS makes it possible to do RF sweeps
quickly.
The benefits of DDS are:
* The ability to generate
arbitrary frequencies with accuracy and stability, limited only by the
oscillator used to clock the phase accumulator. Crystal oscillators, depending
on their specifications, can deliver tolerances of 50 parts per million to ~0.1
part per billion, making DDS extremely accurate. Analog signal generators can
only deliver accuracy and stability of a few tenths of a percent unless using a
high-end device.
* The frequencies provided by
DDS are repeatable. Loading the tuning word register with the value
corresponding to frequency F1 generates a signal at frequency F1. If the tuning
register is then loaded with the value for frequency F2, the output signal is
quickly changed to frequency F2. When the tuning register is reloaded with the
value for F1, the exact the same frequency F1 is provided as was generated
before. Analog generators can't guarantee this precision.
* High frequency resolution
can be achieved with the digital techniques used in DDS. Increasing the
resolution is as simple as adding more bits to the least significant end of the
phase accumulator and tuning register. Analog waveform generators, which depend
on mechanical components like potentiometers and variable capacitors to tune
the oscillator, are limited in the resolution they can provide.
This ability to quickly
change the output frequency with precision is also essential in communication
techniques like spread-spectrum frequency hopping where radio signals are
transmitted by rapidly switching a carrier among many frequency channels. Being
able to reproduce exact frequencies and deliver frequency changes quickly forms
the basis of the modulation technique.
Synthesizing the Signal
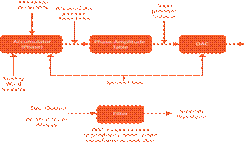
The block diagram for a
representative DDS system is shown in Figure 1.
.
Figure 1
A DDS circuit includes a
phase accumulator, a phase-amplitude table (a lookup table usually in ROM - the
"template") and a digital to analog converter
(DAC). The phase accumulator combines the reference frequency and the value in
the tuning word register. The output from the DAC is usually applied to filters
to smooth the waveform and remove any extraneous output.
The steps to generating a
signal are:
1. The reference signal and
tuning register update the phase accumulator, providing a phase value
2. The corresponding
amplitude for that phase is retrieved from the phase-amplitude table
3. The DAC converts the
retrieved amplitude values to an analog output
4. The output is sent through
smoothing filter
Digital circuits do this
quickly with minimum lag when changing frequencies.
Note: DDS techniques have
been known for some time, but the frequencies that could be provided were
limited by the accuracy of the DAC and the filter (usually a low pass filter with
a capacitor and inductor). With advances in integrated chip technology and
manufacturing, DDS can provide frequencies that are useful for a wide variety
of applications and available on single chip devices. Tools are available to
easily program DDS devices and they can be incorporated into field-programmable
gate arrays (FPGAs). Two popular chips are Analog Devices' AD9833 or AD9850.
Used in a DDS context, the
term reference frequency is used differently than in other engineering
applications. The reference frequency is a clock which controls the rate the
phase accumulator is updated and subsequently the rate the lookup is performed.
Usually provided by a crystal oscillator which clocks the phase accumulator,
some designers use the system clock as the reference. The reference frequency
affects the generated signal; the output is proportional. Doubling the
reference frequency will double the output frequency (when keeping the phase
accumulator, table values and tuning word the same.)
The tuning word is used to
change the output frequencies during operation. The tuning word is a binary
value held in the tuning register. The value of the tuning word is added to the
phase accumulator with every clock update. For example, if the tuning word is
set to 1, every clock interval increments the phase accumulator by 1. Setting
the tuning word to 2, every clock cycle increments the phase accumulator by 2.
Since the phase accumulator
provides the phase value for the phase-amplitude lookup, the tuning word
controls the number of values retrieved from the phase-amplitude table for a
cycle. With a tuning word of 1, every value in the table is retrieved. A tuning
word of 2 reads every other value and also causes the accumulator to clock
through to zero twice as fast, with the result that the output frequency has
been doubled.
As an example, consider a DDS
designed with a phase-amplitude table of 360 entries, holding the amplitude
(voltage) values for each one of the 360 degrees of a sine wave. The
accumulator resets after 360 clock cycles. The reference frequency will be
pulled from the system clock, so everything is clocked and updated at the same
rate. With a tuning word of 1, the phase accumulator is incremented by 1 for
every clock, and the table values are retrieved in order. Every 360 reference
clocks, the accumulator resets and another waveform is created. Setting the
tuning word to 2 has the result of reading every other value from the
phase-amplitude table; the accumulator clocks through twice as fast and the
output frequency is doubled. Of course, using only 360 values would produce a
choppy output and the jitter would make it unusable. DDS systems typically have
phase-amplitude tables with thousands of data points and 16-bit registers for
the tuning register and phase accumulators.
The template values are
important in DDS systems. Just like in digital recording and playback, the
quality of the playback is dependent on the fidelity of the recorded medium and
the playback circuits. No matter how great the playback equipment though, it
can't compensate for a terrible recording. In the same way, a waveform template
used in DDS has to have been digitized (sampled and recorded) to a capture good
signal without distortions.
The templates are built by
digitizing signals using sampling and quantizing techniques and are encoded
into a specific format. The background for digitizing and sampling signals to
be able to recreate them lies in communications theory and how much information
is required to accurately recreate a signal. As communications progressed to
attempting to transmit signals in a digitized format and then recreating
the analog signal at the receiver end, this
became an issue. Harry Nyquist, working at Bell Labs, found that for
band-limited signals (like voice) the sampling rate had to be twice the highest
frequency used to accurately recreate the signal. Sampled at too low a
frequency, the data points might belong to any number of signals at various
frequencies. Sampling at too high a frequency produced more data, taking up
resources but yielding no better results. This frequency is referred to as the
Nyquist Frequency and is the minimum frequency the original signal must be
sampled at to capture enough data points to recreate a specific signal.
Angles and Waveforms
Although DDS can be used to
provide any periodic waveform, like sine, cosine, ramp, and pulse, we'll look
at how a sine wave is synthesized from voltage values stored in memory. Why can
one waveform template produce signals at different frequencies?
Figure 2a shows a basic
trigonometric phase diagram where a sine wave is shown as a projection from a
circle representing the phase of the waveform. The maximum voltage amplitude
for the sine wave is the radius of the circle. For this discussion, we'll take
the maximum voltage to be one for simplicity. As the phase angle ϴ
advances counterclockwise, there is a
corresponding value of voltage. One complete rotation is 2*Pi radians. No
matter how many times around, the same voltage corresponds the a specific angle ϴ. The frequency of the sine
wave produced depends on how quickly rotations through 2*Pi are completed (the
angular velocity, ω).
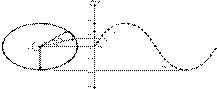
Figure 2a.
Phase Diagram

Figure 2b.
Phase Detail
Figure 2b shows how for each
phase, the specific voltage is sampled. The more points provided for the
waveform by the sampling techniques used, the more definition the waveform has.
The phase-amplitude table holds the phase/voltage points for each waveform and
functions as a phase to voltage converter.
Frequency is related to
angular velocity by the formula:
Frequency=angular velocity(ω)2π Frequency=angular velocity(ω)2π
The frequency is the
reciprocal of the period (T) but by using the phase rather than a time-based
measurement to capture voltage values, the repetitive nature of a waveform can
be exploited. The higher the angular velocity (the quicker the rotations of
angle ϴ shown in Figure 2a), the higher the frequency. As shown in Figure
3, even though the frequency of a waveform changes, the voltage amplitudes are
the same.
Wave 1 goes though a complete cycle, T, in 2*Pi radians. Wave 2
has a cycle equal to the period of T/4, yielding a frequency four times that of
Wave 1, but the amplitude values for the waveforms are the same. To provide
different frequencies, values from the phase-amplitude table are output in a
given time cycle. Any frequency can be generated depending on how many times
the values in the phase-amplitude table are cycled through in a given time
frame.

Figure 3.
Different Frequencies, Same Values
In the DDS context, the
tuning register and accumulator act to 'simulate' the phase rotation of the
waveform. As the accumulator counts through and resets, another cycle is
generated. Setting the tuning word to higher values clock through the table
quicker to provide higher output frequencies. By changing the tuning word, the
phase increment and therefore the frequency can be quickly changed since
there's no settling time required with DDS.
Issues
As noted above, the
phase-amplitude table is a big part of DDS. If the original waveforms were
sampled at a rate that was too low for a desired frequency, an alias distortion
may be seen in the output, with additional frequency components seen around the
desired frequency or the clock frequency. The sampling rate should be at or
above the Nyquist Frequency. If the sampled frequency can't be raised, extra
filtering may be required to remove excessive outputs.
If the precision of the
accumulator is too low, a jitter may be seen in the output, a result of the
jumping from one point on the waveform to another not being smooth enough.
Using the highest possible precision for the accumulator, tuning register and
phase-amplitude table can help minimize jitter, with filtering and digital
processing techniques used for remaining signal definition.
Summary
DDS provides a way to
generate analog signals from values stored
in memory using digital techniques. By changing a tuning register value,
frequencies can be changed quickly without settling time, making it ideal for
testing, communications and frequency sweep applications.